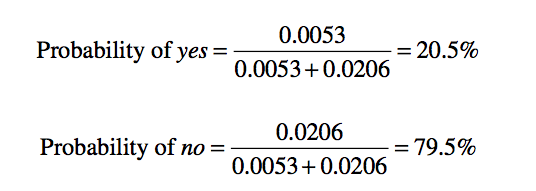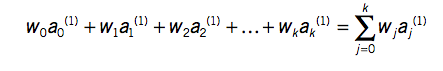The input to a machine learning scheme is a set of
instances. These instances are the things that are to be classified or associated or clustered
Each
instance that provides the input to machine learning is characterized by its values on a fixed, predefined set of
features or
attributes The
value of an
attribute for a particular
instance is a measurement of the quantity to which the
attribute refers
There is a broad distinction between
quantities that are
numeric and ones that are
nominal. Numeric attributes, sometimes called
continuous attributes, measure numbers—either real or integer valued.
Nominal attributes are sometimes called categorical, enumerated, or discrete – näiteks peretüüp, silmade värv, sugu.
a process of
flattening that is techni- cally called
denormalization Output
A linear regression 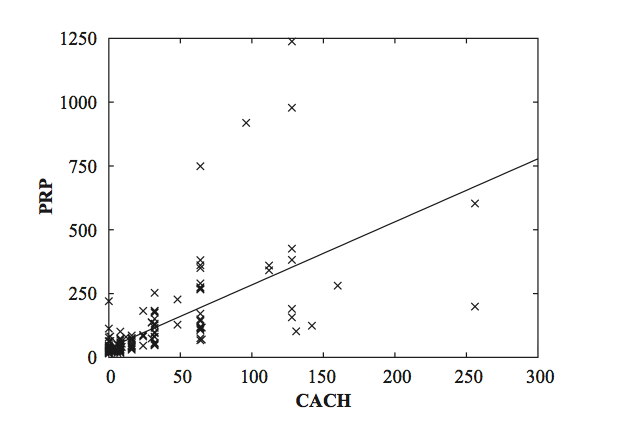
Linear models can also be applied to binary classification problems. In this case, the line produced by the model separates the two classes: It defines where the deci- sion changes from one class value to the other. Such a line is often referred to as the decision boundary.
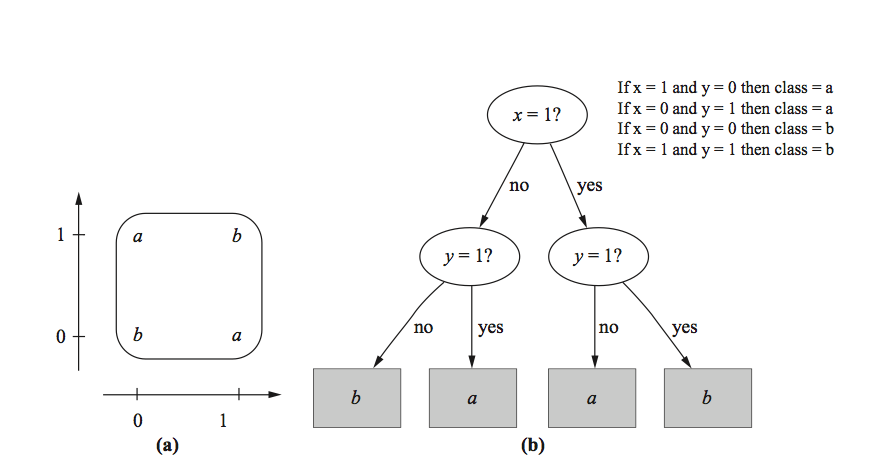
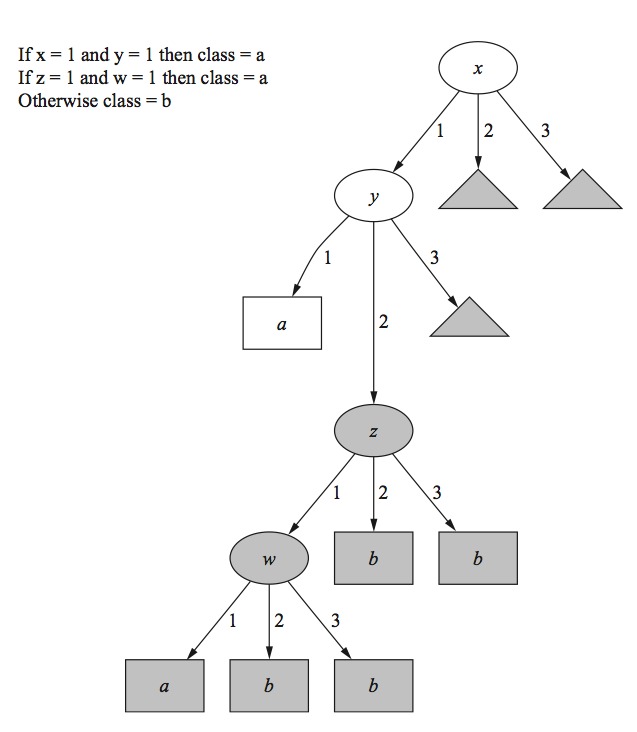
In
instance-based classification, each new instance is compared with existing ones using a distance metric, and the closest existing instance is used to assign the class to the new one. This is called the
nearest-neighbor classification method. Sometimes more than one nearest neigh- bor is used, and the majority class of the closest k neighbors (or the distance- weighted average if the class is numeric) is assigned to the new instance. This is termed the
k-nearest-neighbor method
Deriving suitable attribute weights from the training set is a key problem in instance-based learning
Methods
Naïve Bayes
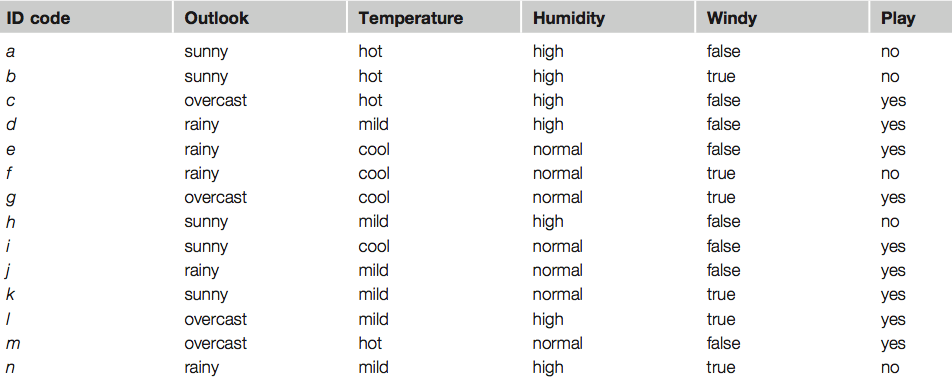
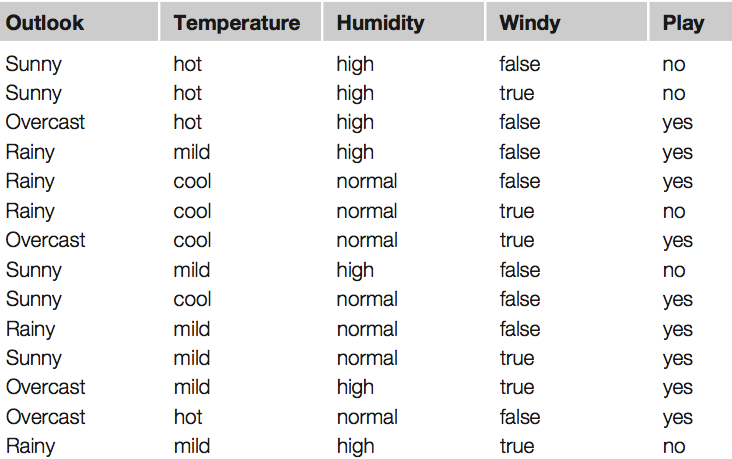
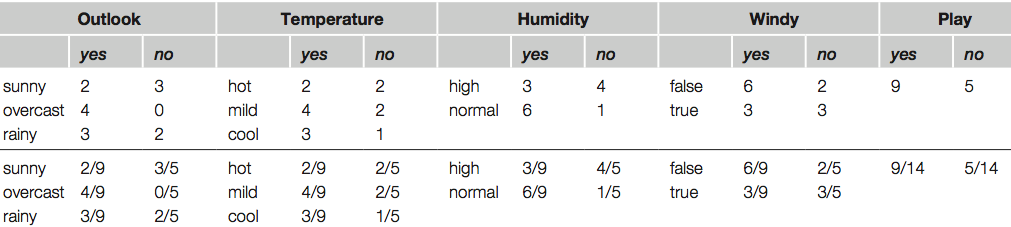
Table shows a summary of the weather data obtained by counting how many times each attribute–value pair occurs with each value (yes and no) for play
Likelihood of yes = 2/9×3/9×3/9×3/9×9/14 = 0.0053
Likelihood of no = 3/5 × 1/5 × 4/5 × 3/5 × 5/14 = 0.0206
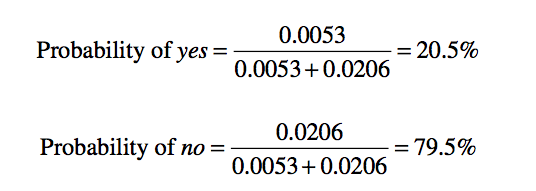
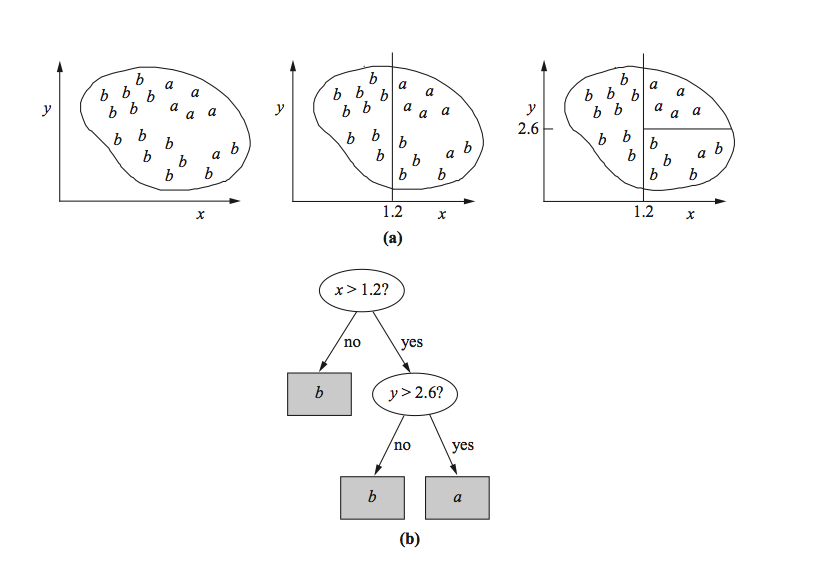
Tree 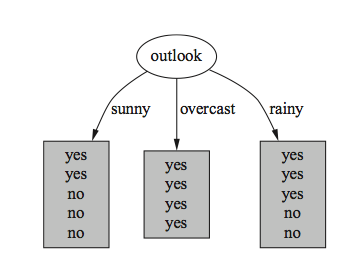
Outlook= sunny: info((2,3))= entropy(2/5,3/5) = -2/5 * log(2/5) – 3/5 * log(3/5) = 0.971 bits
Outlook = overcast: info((4,0)) = entropy(1,0) = -1 * log(1) – 0 * log(0) = 0 bits
Outlook = rain: info((3,2)) = entropy(3/5, 2/5) = -3/5 * log(3/5) – 2/5 * log(2/5) = 0.971 bits
Expected info for Outlook = Weighted sum of the above: info((3,2),(4,0),(3,2)) = 5/14 * 0.971 + 4/14 * 0 + 5/14 * 0.971 = 0.693
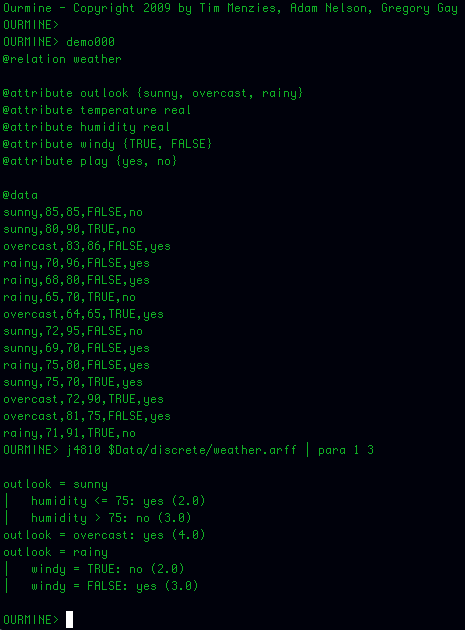
Pisike käsurea utiliit otsustuspuu genereerimiseks
Veel üks alternatiivne variant tree genereerimiseks
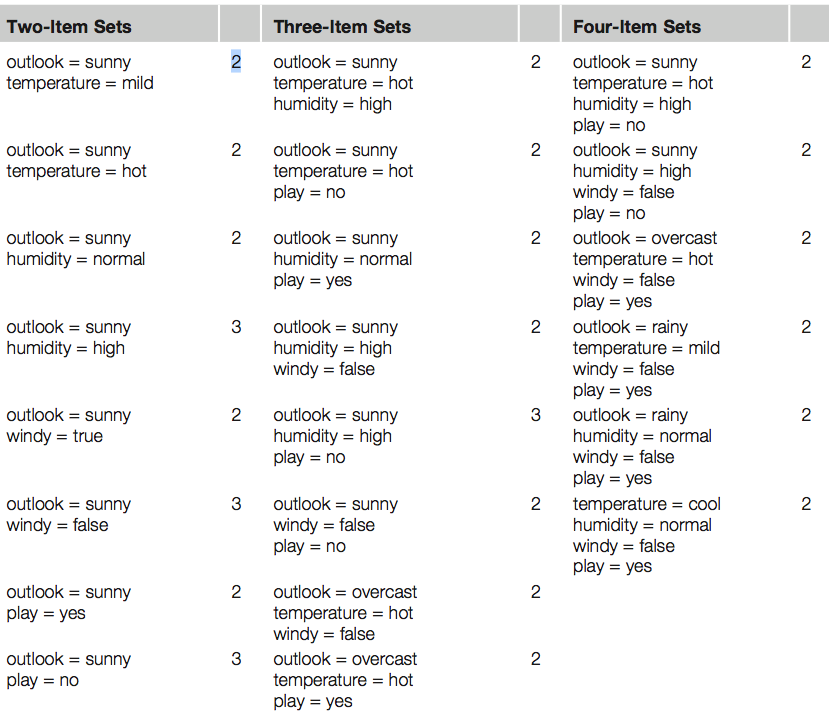
Otsime nn ItemSet paare. Otsime paare, mis tekivad minimaalselt kahel tingimusel.
Näiteks üks kahele tingimusele vastav paar oleks Outlook=Sunny, Temperature=hot
Kolmene paar oleks Outlook= Sunny, Temperature=hot, Humidity=high
Neljase paari näide Outlook=Sunny, Temperature=hot, Humidity=high, Play=no
Kirjeldame, mitu paari me leiame. Näiteks neljast item-set paari (Outlook=Sunny, Temperature=hot, Humidity=high, Play=no) leiame kahel korral.
Saame alloleva tabeli
Genereerime reeglid
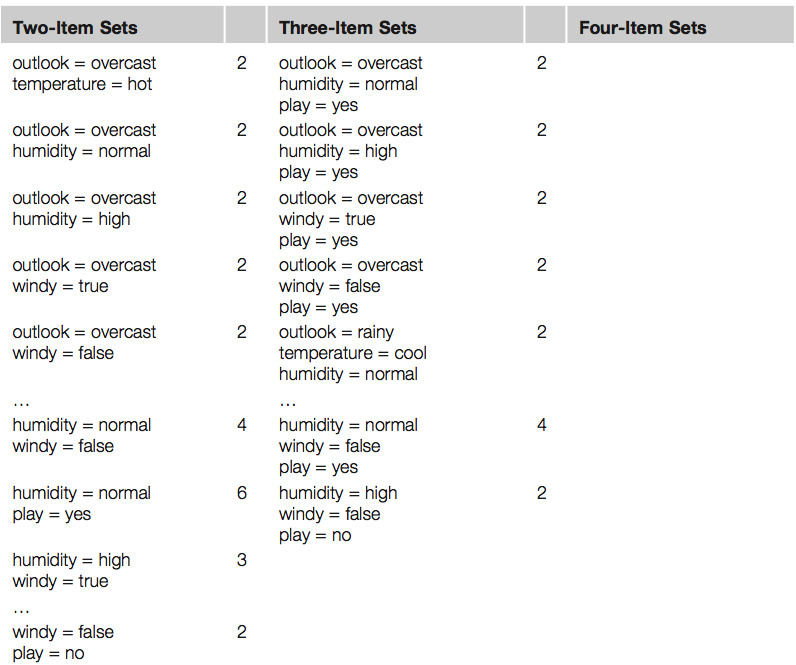
Võtame näiteks ühe kolmese paari – humidity = normal, windy = false, play = yes ja vaatame milliseid tingimusi sealt annab genereerida.
Lisaks paneme kirja mitu korda mingi tingimus esineb ja mitmel korral ta on tõene.
humidity = normal, windy = false, play = yes If humidity = normal and windy = false then play = yes 4/4 (iga paar annab play = yes / neli paari humidity = normal and windy = false e 4/4 –
coverage) 4/4 = 1 ehk 100%
accuracy If humidity = normal and play = yes then windy = false 4/6 ( 4 kord kuuest tingimusest humidity = normal and play = yes on tõene windy = false) 4/6 –
coverage, (0.66) 70% accuracy If windy = false and play = yes then humidity = normal 4/6 If humidity = normal then windy = false and play = yes 4/7 If windy = false then humidity = normal and play = yes 4/8 If play = yes then humidity = normal and windy = false 4/9 If – then humidity = normal and windy = false and play = yes 4/14 – siin näiteks on tingimus humidity = normal and windy = false, mis ilmneb 14 korral ainult 4 korral tõene. Kui me nüüd seame tingimuseks et minimaalne coverage on 2 ja minimaalne accuracy = 100% siis saame 58 reeglit. Mõned neist allpoolt toodud tabelis
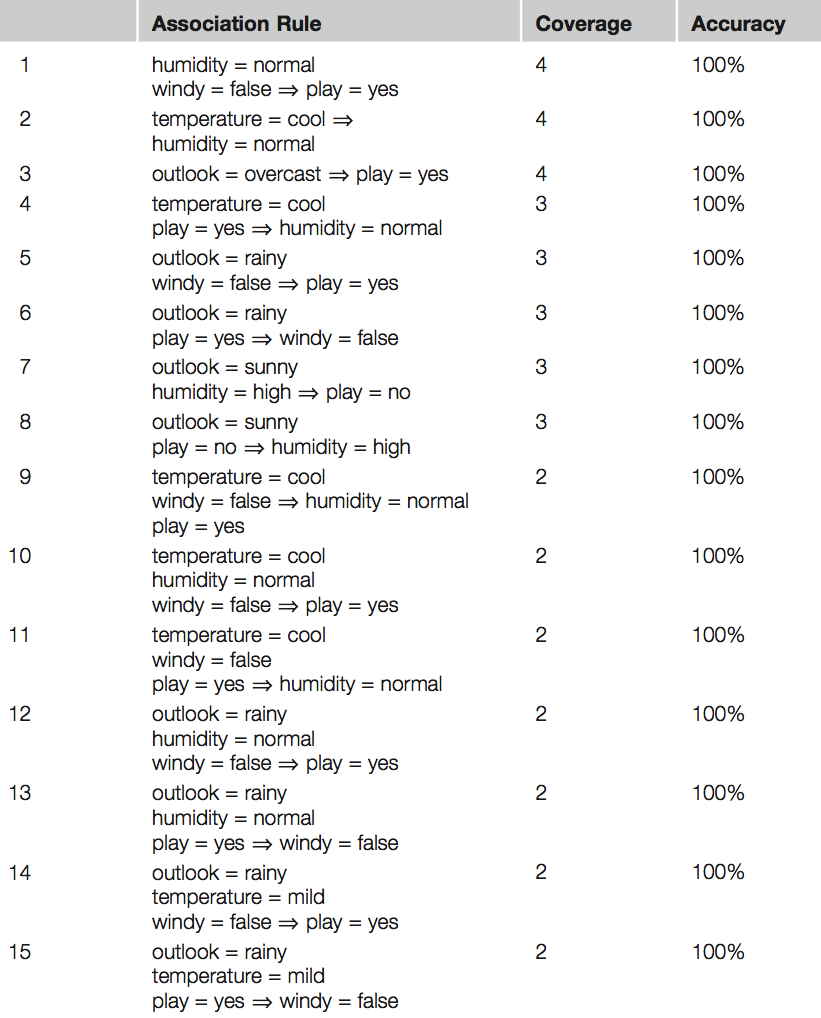
…

Weka solution to generate rules

Numeric Prediction: Linear Regression (supervised) Kui andmed on numbrilised/skalaarid, siis
linear regression on üks meetoditest, mida kaaluda.
x=w0 +w1*a1 +w2*a2 +…+wk*ak x – class a0, a1,a2,…, ak – attribute values (a0 is always 1 –
bias) w0, w1,…., wk – weights (are calculated from the training data)
The predicted value for the first instance’s class can be written as
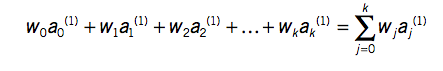
antud valem ei anna mitte klassi väärtust vaid ennustatud klassi. Tuleb hakata võrdlema viga, mis on reaalse klassi ja ennustatud klassi vahel 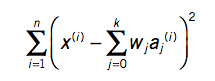 Erinevaid online linear regression tööriistasid on olemas (http://www.wessa.net/slr.wasp) Üks näide X, Y 1,1 1,2 2,1 2,3 2,4 4,3 4,4
Erinevaid online linear regression tööriistasid on olemas (http://www.wessa.net/slr.wasp) Üks näide X, Y 1,1 1,2 2,1 2,3 2,4 4,3 4,4 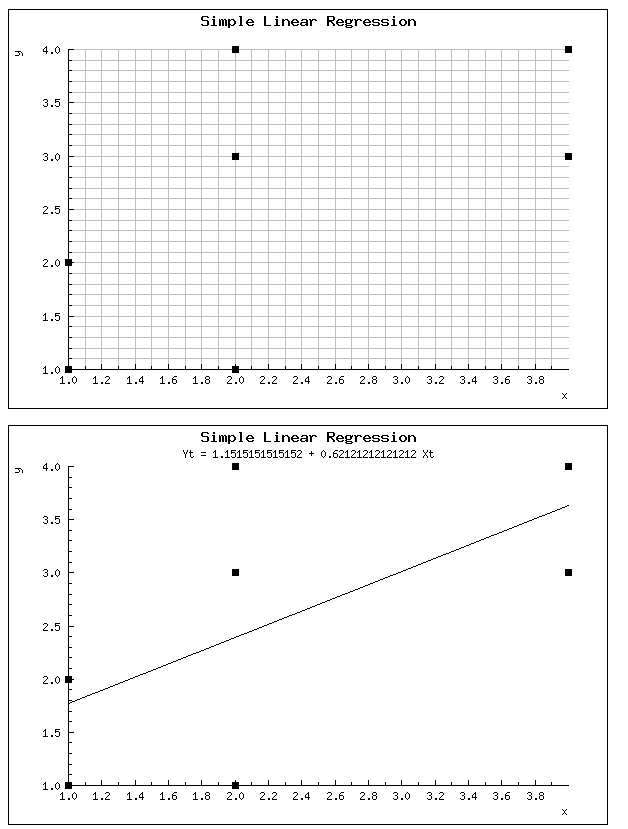 wolfram alfa
wolfram alfa 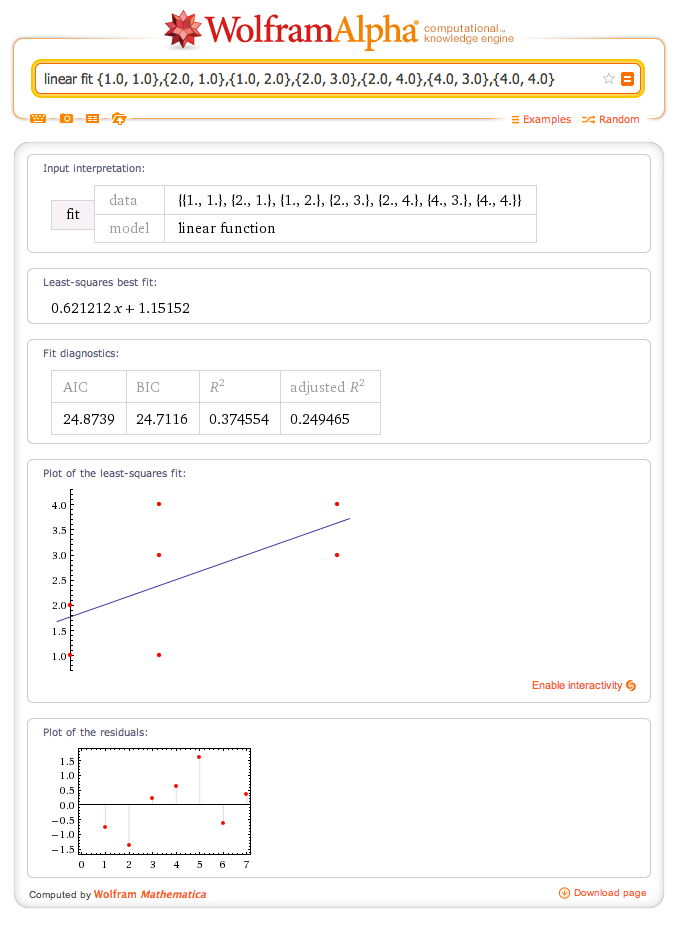
Of course, linear models suffer from the disadvantage of, well,
linearity
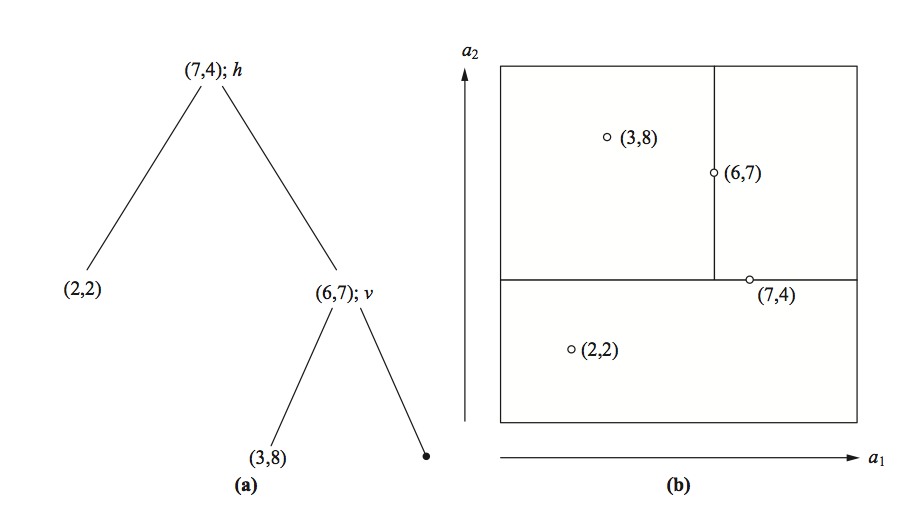
K-Nearest neighbors (supervised) training data and generated tree (k = 2 )
Clustering (unsupervised)
techniques apply when there is no class to be predicted but the instances are to be divided into natural groups
The classic clustering technique is called
k-means
Support vector machines select a small number of critical boundary instances called support vectors from each class and build a linear discriminant function that separates them as widely as possible. This instance-based approach transcends the limitations of linear boundaries by making it practical to include extra nonlinear terms in the function, making it possible to form quadratic, cubic, and higher-order decision boundaries
e ja f on väga sarndased

The function (x • y)^n, which computes the dot product of two vectors x and y and raises the result to the power n, is called a polynomial kernel.
Other kernel functions can be used instead to implement different nonlinear mappings. Two that are often suggested are the radial basis function (RBF) kernel and the sigmoid kernel. Which one produces the best results depends on the applica- tion, although the differences are rarely large in practice. It is interesting to note that a support vector machine with the RBF kernel is simply a type of neural network called an RBF network (which we describe later), and one with the sigmoid kernel implements another type of neural network, a multilayer perceptron with one hidden layer.
Mathematically, any function K(x, y) is a kernel function if it can be written as K(x, y) = ?(x) • ?(y), where ? is a function that maps an instance into a (potentially high-dimensional) feature space. In other words, the kernel function represents a dot product in the feature space created by ?
Just one k-mean picture
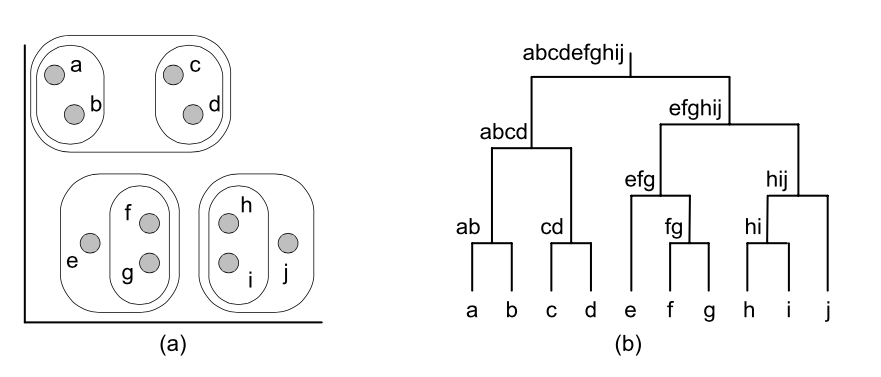
 …
…  Weka solution to generate rules
Weka solution to generate rules 
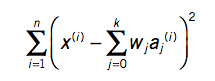 Erinevaid online linear regression tööriistasid on olemas (http://www.wessa.net/slr.wasp) Üks näide X, Y 1,1 1,2 2,1 2,3 2,4 4,3 4,4
Erinevaid online linear regression tööriistasid on olemas (http://www.wessa.net/slr.wasp) Üks näide X, Y 1,1 1,2 2,1 2,3 2,4 4,3 4,4  wolfram alfa
wolfram alfa