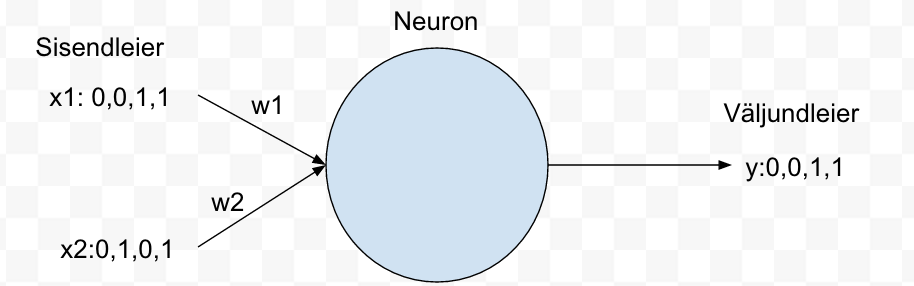
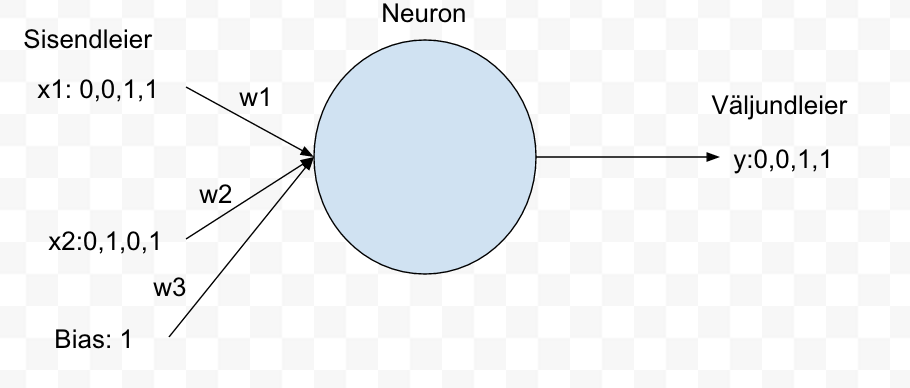
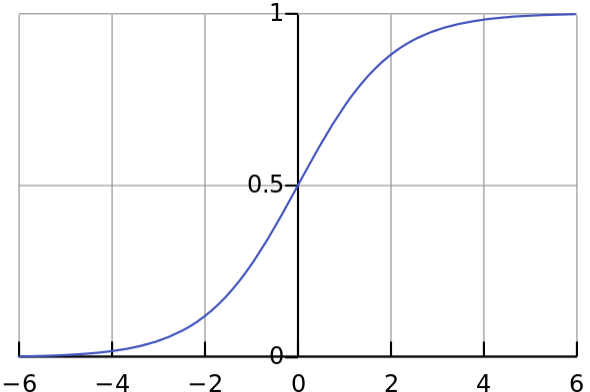
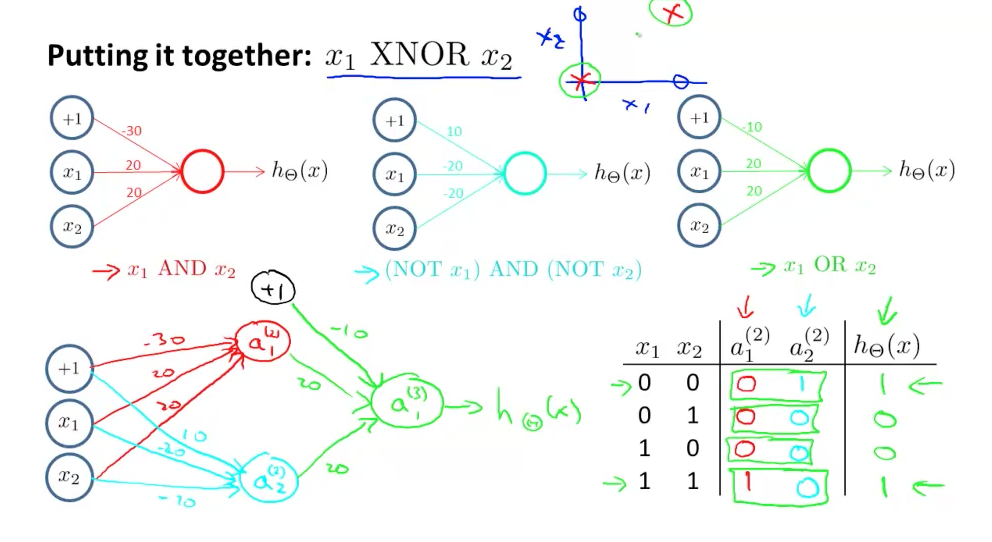
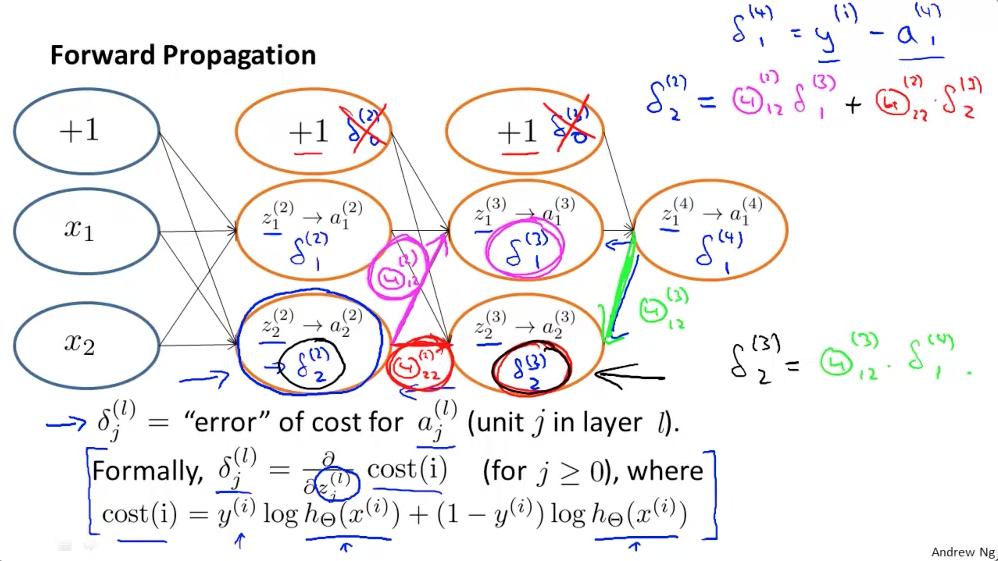
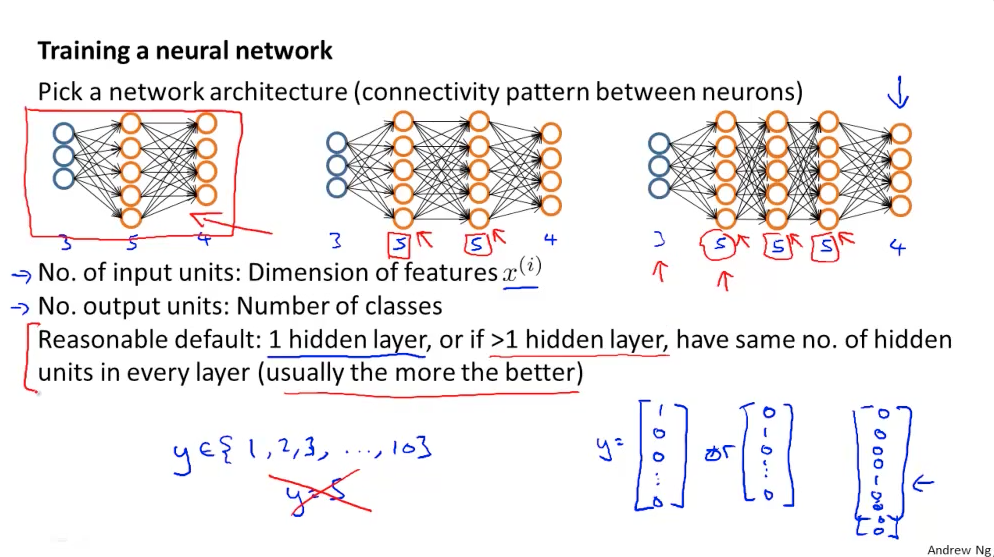
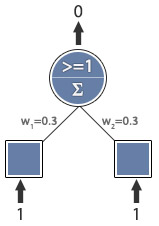
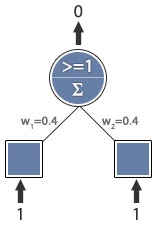
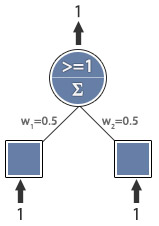
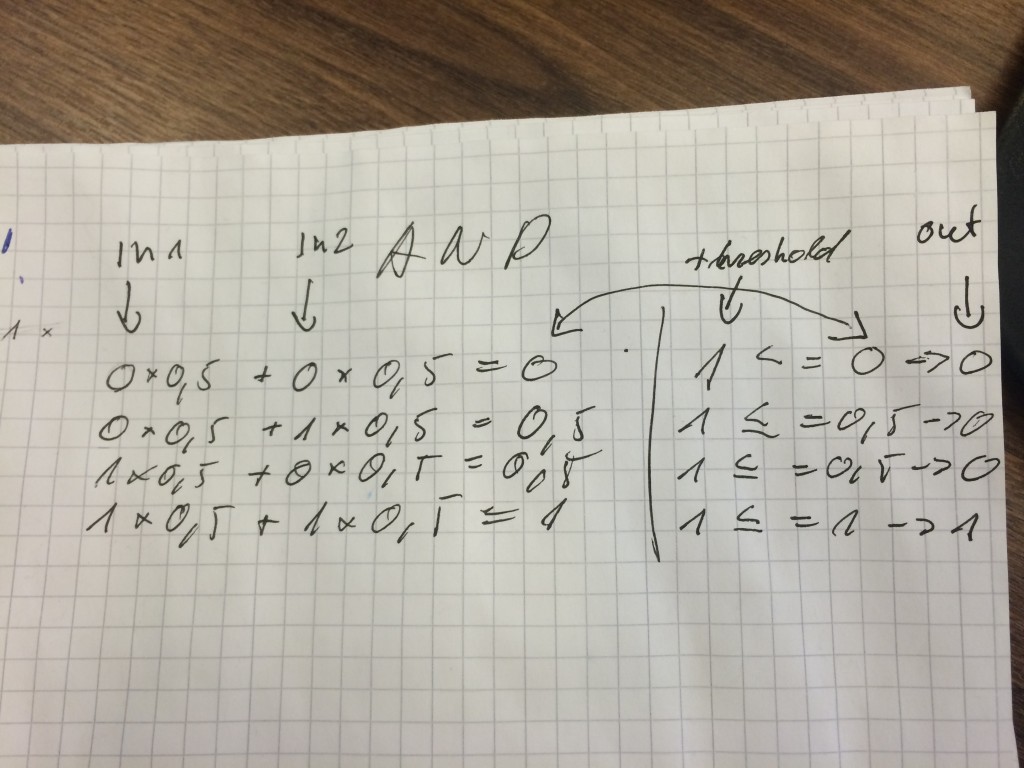
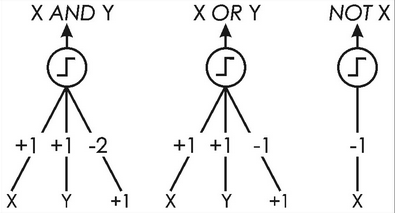
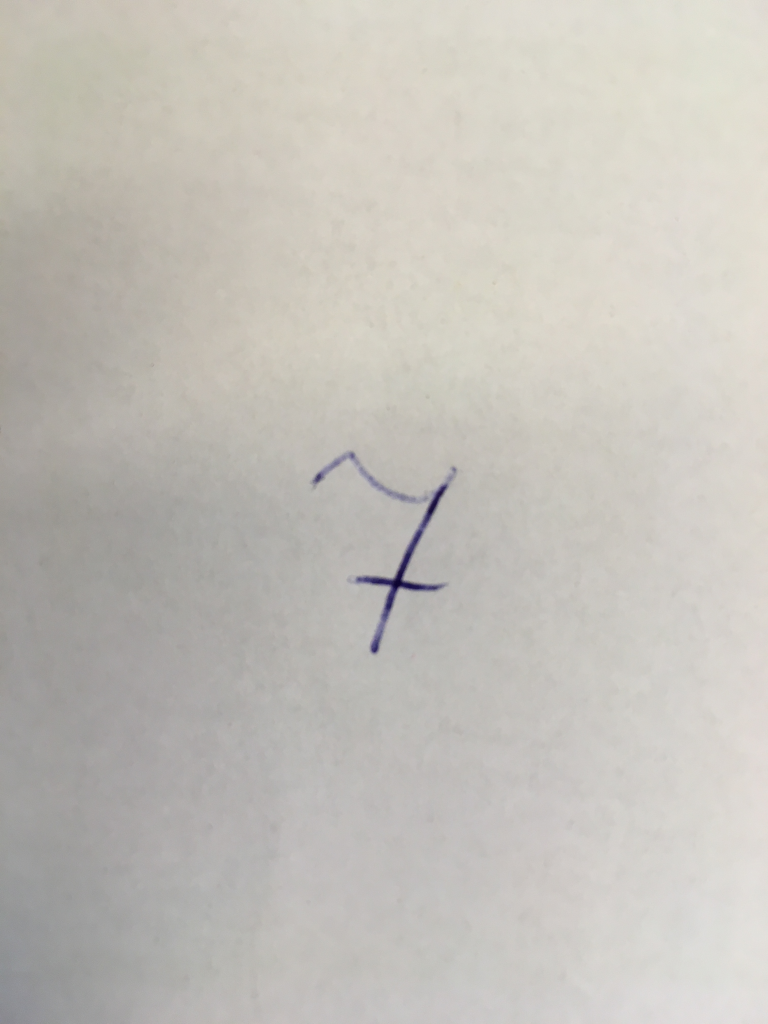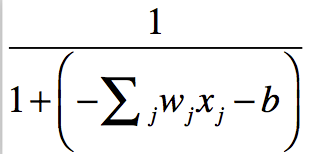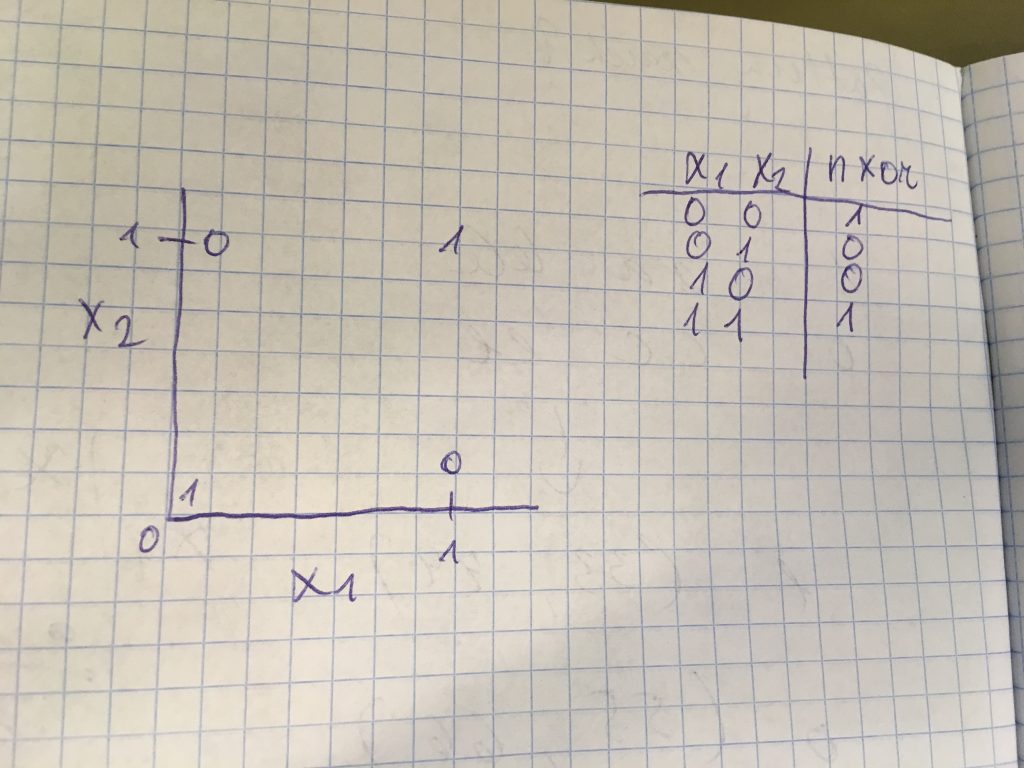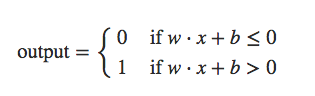Machine Learning – Margus Roo

Motion detection with OpenCV

Posted on May 23, 2017 by margusja

Olen alati aukartusega vaadanud laenurgas seisvadi automaatseid tulelüliteid, mis liikumise tuvastades lülitavad valguse sisse ja mõne aja pärast taas valguse välja lülitavad. Fantastilised seadmed.

Kuidas nad seda teevad? Variante on mitmeid, ühte neist katsetasin ka ise.

Natukene teooriat – https://en.wikipedia.org/wiki/Background_subtraction

Mina kasutasin OpenCV raamistiku opencv2/video/background_segm.hpp, mis analüüsib videosisendit (pildijada) ja lihtsustatult võttes võrdleb eelmisi pilte praegusega. Liikumise puudumisel on ajalugu suht sarnane. Liikumise olemasolul teatud regioonide ajalugu ei ole sarnane ja antud meetod ka selle siis visualiseerib.

Image to matrix using ImageMagick

Posted on October 3, 2016 - October 3, 2016 by margusja

I have example picture

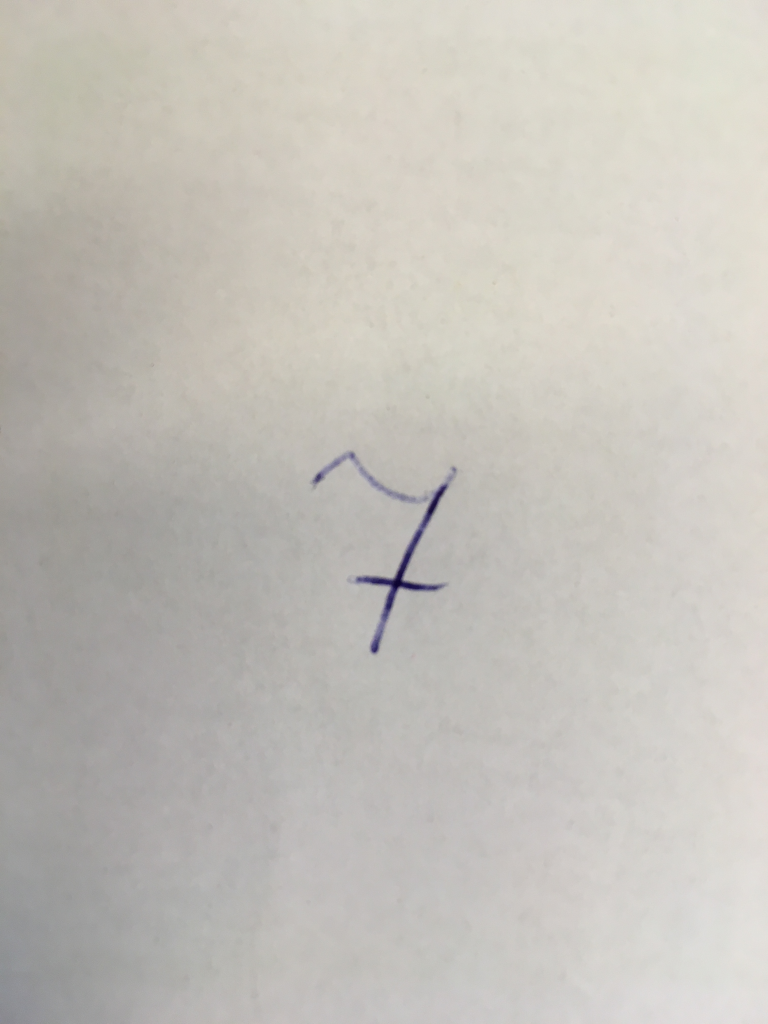
Now I converted it in to 28×28 image

ImageMagick:

Original:

[margusja@bigdata18 ~]$ identify seven_28_28.png
seven_28_28.png PNG 527×524 527×524+0+0 8-bit DirectClass 13KB 0.000u 0:00.000

[margusja@bigdata18 ~]$ convert seven_28_28.png -resize 28×28 seven_28_28_new.png

28×28 pixel image

[margusja@bigdata18 ~]$ identify seven_28_28_new.png
seven_28_28_new.png PNG 28×28 28×28+0+0 8-bit DirectClass 1.7KB 0.000u 0:00.000

Take image as a text

[margusja@bigdata18 ~]$ convert seven_28_28_new.png txt:-

0,0: (209,203,196,255) #D1CBC4 srgba(209,203,196,1)
1,0: (210,204,197,255) #D2CCC5 srgba(210,204,197,1)
2,0: (209,203,195,255) #D1CBC3 srgba(209,203,195,1)
3,0: (207,201,193,255) #CFC9C1 srgba(207,201,193,1)
4,0: (206,202,194,255) #CECAC2 srgba(206,202,194,1)
5,0: (210,205,197,255) #D2CDC5 srgba(210,205,197,1)
6,0: (210,205,198,255) #D2CDC6 srgba(210,205,198,1)
7,0: (203,198,195,255) #CBC6C3 srgba(203,198,195,1)
8,0: (191,187,189,255) #BFBBBD srgba(191,187,189,1)
9,0: (186,182,184,255) #BAB6B8 srgba(186,182,184,1)
10,0: (203,196,192,255) #CBC4C0 srgba(203,196,192,1)
11,0: (208,202,194,255) #D0CAC2 srgba(208,202,194,1)
12,0: (207,202,194,255) #CFCAC2 srgba(207,202,194,1)
13,0: (209,204,196,255) #D1CCC4 srgba(209,204,196,1)
14,0: (210,205,196,255) #D2CDC4 srgba(210,205,196,1)
15,0: (210,204,196,255) #D2CCC4 srgba(210,204,196,1)
16,0: (211,204,196,255) #D3CCC4 srgba(211,204,196,1)
17,0: (211,205,196,255) #D3CDC4 srgba(211,205,196,1)
18,0: (212,205,197,255) #D4CDC5 srgba(212,205,197,1)
19,0: (212,205,197,255) #D4CDC5 srgba(212,205,197,1)
20,0: (211,205,196,255) #D3CDC4 srgba(211,205,196,1)
21,0: (214,206,198,255) #D6CEC6 srgba(214,206,198,1)
22,0: (215,208,199,255) #D7D0C7 srgba(215,208,199,1)
23,0: (213,206,198,255) #D5CEC6 srgba(213,206,198,1)
24,0: (213,206,198,255) #D5CEC6 srgba(213,206,198,1)
25,0: (213,206,198,255) #D5CEC6 srgba(213,206,198,1)
26,0: (213,206,198,255) #D5CEC6 srgba(213,206,198,1)
27,0: (215,209,201,255) #D7D1C9 srgba(215,209,201,1)

…

0,27: (198,194,192,255) #C6C2C0 srgba(198,194,192,1)
1,27: (199,195,192,255) #C7C3C0 srgba(199,195,192,1)
2,27: (199,196,191,255) #C7C4BF srgba(199,196,191,1)
3,27: (195,193,189,255) #C3C1BD srgba(195,193,189,1)
4,27: (194,193,189,255) #C2C1BD srgba(194,193,189,1)
5,27: (196,194,191,255) #C4C2BF srgba(196,194,191,1)
6,27: (200,198,195,255) #C8C6C3 srgba(200,198,195,1)
7,27: (201,199,195,255) #C9C7C3 srgba(201,199,195,1)
8,27: (201,199,196,255) #C9C7C4 srgba(201,199,196,1)
9,27: (202,201,198,255) #CAC9C6 srgba(202,201,198,1)
10,27: (203,202,198,255) #CBCAC6 srgba(203,202,198,1)
11,27: (203,202,198,255) #CBCAC6 srgba(203,202,198,1)
12,27: (203,201,197,255) #CBC9C5 srgba(203,201,197,1)
13,27: (203,202,198,255) #CBCAC6 srgba(203,202,198,1)
14,27: (204,203,198,255) #CCCBC6 srgba(204,203,198,1)
15,27: (205,204,199,255) #CDCCC7 srgba(205,204,199,1)
16,27: (204,202,198,255) #CCCAC6 srgba(204,202,198,1)
17,27: (204,203,199,255) #CCCBC7 srgba(204,203,199,1)
18,27: (204,203,199,255) #CCCBC7 srgba(204,203,199,1)
19,27: (203,201,197,255) #CBC9C5 srgba(203,201,197,1)
20,27: (203,200,196,255) #CBC8C4 srgba(203,200,196,1)
21,27: (204,200,197,255) #CCC8C5 srgba(204,200,197,1)
22,27: (204,201,198,255) #CCC9C6 srgba(204,201,198,1)
23,27: (204,202,198,255) #CCCAC6 srgba(204,202,198,1)
24,27: (206,203,198,255) #CECBC6 srgba(206,203,198,1)
25,27: (208,204,200,255) #D0CCC8 srgba(208,204,200,1)
26,27: (207,204,200,255) #CFCCC8 srgba(207,204,200,1)
27,27: (209,207,203,255) #D1CFCB srgba(209,207,203,1)

More easily working data

[margusja@bigdata18 ~]$ convert seven_28_28_new.png -colorspace gray seven_28_28_gray.png

[margusja@bigdata18 ~]$ convert seven_28_28_gray.png txt:- | more | awk {‘print $1 ” ” substr($2, 2, 3)’}

0,0: 154
1,0: 156
2,0: 154
3,0: 150
4,0: 151
5,0: 157
6,0: 157
7,0: 146
8,0: 129
9,0: 121
10,0: 143
11,0: 152
12,0: 152
13,0: 155
14,0: 157
15,0: 156
16,0: 156
17,0: 157
18,0: 158
19,0: 158
20,0: 157
21,0: 160
22,0: 163
23,0: 160
24,0: 160
25,0: 160
26,0: 160
27,0: 164

…

0,27: 139
1,27: 141
2,27: 141
3,27: 136
4,27: 136
5,27: 138
6,27: 144
7,27: 146
8,27: 146
9,27: 149
10,27: 150
11,27: 150
12,27: 149
13,27: 150
14,27: 152
15,27: 154
16,27: 151
17,27: 152
18,27: 152
19,27: 149
20,27: 148
21,27: 149
22,27: 150
23,27: 151
24,27: 153
25,27: 155
26,27: 155
27,27: 159

Apache Spark image recognition result – not bad

Posted on October 3, 2016 - October 5, 2016 by margusja

evaluator: org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator = mcEval_a147352f3495 precision: Double = 0.9735973597359736 confusionMatrix: org.apache.spark.sql.DataFrame = [label: double, 0.0: bigint, 1.0: bigint, 2.0: bigint, 3.0: bigint, 4.0: bigint, 5.0: bigint, 6.0: bigint, 7.0: bigint, 8.0: bigint, 9.0: bigint] Confusion Matrix (Vertical: Actual, Horizontal: Predicted): +-----+---+----+----+---+---+---+---+---+---+---+ |label|0.0| 1.0| 2.0|3.0|4.0|5.0|6.0|7.0|8.0|9.0| +-----+---+----+----+---+---+---+---+---+---+---+ | 0.0|961| 0| 3| 2| 1| 4| 5| 2| 1| 1| | 1.0| 0|1125| 4| 0| 0| 1| 1| 2| 2| 0| | 2.0| 3| 2|1005| 5| 1| 1| 2| 4| 9| 0| | 3.0| 0| 0| 3|992| 0| 1| 0| 4| 6| 4| | 4.0| 2| 0| 4| 1|953| 1| 3| 3| 2| 13| | 5.0| 6| 0| 0| 15| 1|858| 5| 1| 4| 2| | 6.0| 4| 2| 3| 0| 5| 8|936| 0| 0| 0| | 7.0| 0| 5| 9| 3| 1| 0| 0|992| 1| 16| | 8.0| 3| 0| 4| 6| 2| 6| 3| 5|944| 1| | 9.0| 2| 2| 2| 10| 11| 2| 2| 6| 3|969| +-----+---+----+----+---+---+---+---+---+---+---+

About visualization. One way to present results is above. But much more nicer is in example graph from apache-zeppelin sql node:

What we can see from picture. In example we are on number zero and we can see that number of correct predictions is 961. Also there is a list of wrongly predicted numbers.

In the next picture when we hover over 5 we can see there is red area top of it. As you can see red in this picture means number 5. So there are 15 wrongly predicted numbers as number 3. And it is expected because numbers 5 and 3 are quite similar for machine.

tf–idf – term frequency inverted document frequency

Posted on September 27, 2016 by margusja

Paari sõnaga enda jaoks, et meelest ei läheks.

tf-idf on meetod dokumentide (tekstide) ja üksiku sõna vahelise tähtsuse arvutamiseks.

Võtame näiteks lause: “Matemaatika on teaduste alus”. Lisaks on meil terve raamatukogutäis tekste. Kui me soovime saada meie lausele parimaid vasteid raamatukogust, siis on üsna suur tahtmine hakata otsima kui mitu korda mõni lause element esineb tekstis. On selge, et sellisel viisil leiame me väga palju meid mitte huvitavaid vasteid, sest sõna “on” esineb ilmselt väga paljudes tekstides ja domineerib. Sellist meetodit nimetatakse tf (term frequency).

Näiteks võtame kaks dokumenti sisuga:

d1: “Matemaatika on teaduste alus. Enamus reaalained on väga vajalikud igapäevaelus”

d2: “Muri on minu koer. Mari jalutab Muriga õues”

Lugedes kokku “on” dokumentides saame – d1: 2 ja d2: 1

Lugedes kokku sõnad dokumentides saame – dw1: 10 ja dw2: 8

Valem tf arvutamiseks on: tf(“on”, d1) = d/dw ehk d1 puhul 2/8 => 1/4 = 0.25 ja d2 puhul 1/8 = 0.125

idf valem on idf = log((kogu dokumentide arv)/(dokumendid, mis sisaldavad otsitavat stringi)) ehk antud näite puhul idf=log(2/2) => log 1 = 0. Ehk antud stringi mõju on väga väike, kuna ta esineb kõikides dokumentides.

Kui valida näidiseks “Matemaatika”, siis idf=log(2/1)=0.3 Samuti on näha, et dokumentide arvu tõustes harva esinevad stringid hakkavad oma kaalu koguma. Näiteks, kui meil oleks kolm dokumenti ja “Matemaatika” oleks esindatud ainult ühes dokumendis, siis idf=log(3/1)=0.477 Nelja dokumendi puhul oleks idf lausa 0.6

Neuron Network notes

Posted on September 24, 2016 - October 7, 2016 by margusja

Kuna arvutusvõimsus on sealmaal, et närvivõrgustiku analoogial välja töötatud tehnoloogia on nüüdseks kasutatav, siis teen enda jaoks taas asja puust ja punaselt ette. Noh, et oleks võtta juhul kui keegi küsib ja jube tark paistan ka välja.

Neuron Network ja Deep Learning on selline tehnoloogia, et väidetavalt saab nende abil lahendada suvalist pidevat funktsiooni. Tingimuseks on vaid piisav arv neuroneid ja hidden layereid. Kõlab paljulubavalt. Seega tasub sellel tehnoloogial silma peal hoida.

Et anda aimu neuron network toimimisest, defineerin lihtsa ülesande. Oletame, et mul on andmetabel kahest sisendist ja väljund.

0 ja 0 annab 0

0 ja 1 annab 0

1 ja 0 annab 1

1 ja 1 annab 1

ehk kaks sisendit ja üks väljund.

Sellise masina ehitamine, mis ülaltoodut realiseeriks oleks kindlasti lihtsam ehitada mõne teise tehnoloogiaga, aga siinkohal sobib antud ülesanne oma lihtsuse tõttu neuron network’i põhimõtet demonstreerima.

Neuron network kontekstis nimetatakse sisendeid ja väljundeid leieriteks (leyer ik.).

Meie sisendleieriks on paarid o,o ; 0,1 ; 1,0 ; 1,1 ja vastavateks väljundleieriteks 0, 0, 1, 1

Kuna on soov ehitada väga lihtne neuron networks, siis lihtsaim, mida ehitada saab on ühe neuroniga võrk (perceptron). Vt joonis 1.

Joonis 1

Üks neuron network’i põhiomadusi on adapteeruda ehk vigadest õppida. Kui me mõnda aega oleme ütelnud oma neuron network’le, et sisend 0,0 ei ole mitte 1 vaid 0, siis lõpuks saab ta sellest aru. Kuidas?

Iga leieri ja neuroni vahel olev ühendus nn kaalutakse. Harilikult vahemikus -1 kuni 1.

Joonisel 2 oleme lisanud ka kaalud w1 ja w2. Ühtlasi tähistasime ka sisendid x1 ja x2 ja väljundi y.

Joonis 2

Nüüd läheme neuroni kallale. Neuron teeb mingi tehte sisenditega ja kaaludega. Võrdleb arvutatud väljundit tegeliku väljundiga. Arvutab vea ja muudab vastavalt saadud veale kaalusid ja alustab otsast peale. Niikaua kuni viga on piisavalt väike e arvutatud väljund on piisavalt sarnane tegelikule väljundile.

Oluline on leida kaalud (w1,w2,w3), mis sobivad kõikide sisendi paaride korral.

Sisendite hulka on lisatud ka bias. Bias on üks võimalusi määrata kui tundlik on väljund. Mida suurem on bias seda lihtsam on neuronil võimalik aktiveeruda. Antud näite juures valime bias=1. Vt joonis 3.

Joonis 3

NB! Juhul kui realiseerida NN programmatiliselt ise, siis peab tähelepanu pöörama asjaolule, et ei valitaks alustamiseks kõike kaalusid näiteks 0 väärtusega või sarnaseid. Sobivad juhuslikud väärtused 0 ja 1 vahel.

Meie lihtne neuron omab arvutust:

algus:

w1 ja w2 = mingid suvalised kaalud vahemikus -1 kuni 1
y=(x1*w1)+(x2*w2)+(bias*w3)
error = õige vastus – y
Kui viga on liiga suur:
- w1 = w1+error*x1
- w2 = w2+error*x2
siis mine tagasi algusesse

lõpp;

Lihtsa programmi abil võin kinnitada, et peale tuhandet iteratsiooni on mul kaalud, mis sobivad iga paari jaoks.

w1:9.67299303, w2:-0.2078435, w3:-4.62963669

Proovime neid:

Paar 0,0:

(0*9.67299303)+(0*-0.2078435)+(1*-4.62963669)=-4,62963669

Paar 0,1

(0*9.67299303)+(1*-0.2078435)+(1*-4.62963669)=-4,83748019

Paar 1,0

(1*9.67299303)+(0*-0.2078435)+(1*-4.62963669)=5,04335634

Paar 1,1

(1*9.67299303)+(1*-0.2078435)+(1*-4.62963669)=4,83551284

Tulemus pole just see, mida ootasime? Nüüd tuleb mängu viimane element neuron network’is – activation function, mis kuulub iga neuroni juurde. Nagu ülalt näha, siis võime kirjeldada kolmikud:

0,0,-4.62963669

0,1,-4.83748019

1,0,5.04335634

1,1,4.83551284

Kui me nüüd laseme kolmikute viimase elemendi läbi lihtsa funktsiooni:

activationFunction (x):

Kui x <= 0 siis väljund 0

muidu väljund 1

end:

0,0,activationFunction(-4.62963669)

0,1,activationFunction(-4.83748019)

1,0,5,activationFunction(5.04335634)

1,1,activationFunction(4.83551284)

teisisõnu:

0,0,0

0,1,0

1,0,1

1,1,1

Kui nüüd selliseid ninaarseid tehteid teostavaid neoroneid omavahel kombineerida, siis saab lahendada suvalise loogikafunktsiooni.

Vot selline tubli loom on see neuron network. Masinad õpivad 🙂

Üleval käsitlesin “perceptron”i ehk sisendiks on 1 või null ja väljund on 0 kui (X1*W1)+(X2*W2)+b <=0 ja väljund on 1 kui (X1*W1)+(X2*W2)+b > 1

Sigmoid neuron

Sarnaneb perceptron’le aga sisendid on 0 ja 1 vahel reaalarvud ja väljundiks on sigmoid funktsioon:

Lihtne näide (mida saab palju lihtsamalt lahendada, aga antud kontekstis siiski ilmekas) on NXOR. Selge on see, et lineaarse funktsiooniga ei ole siin midagi peale hakata.

Siinkohal toon ühe pildi Andrew Ng loengust, kus on näha, kuidas erinevaid binaarseid tehteid kombineerida ning saavutada mittelineaarne väljund.

Allpool on näha, et meil on kaks neuronit hidden kihis, mis realiseerivad erinevaid funktsioone ja mille väljundit tarbib väljundkiht, mis realiseerib mittelineaarse funktsiooni.

Back Propagation

Minu jaoks suht keeruline teema, aga paari sõnaga kuidas mina asjast aru saan.

Kui Forward Propagation on eelmisest (vasakul asuvast) kihist tulevate aktiveerimis funktsioonide väärtuste ja kaalude korrutiste summa -Ai( Sum(A(i-1)*W(i-1))) kus i tähistab aktiivset kihti, siis back propagation puhul on tegu järgnevasse (paremale) kihti suunatud kaalude ja järgneva (parema) kihi cost funktsiooni tulemuste korrutiste summa – Sum(W(i+1)* (Di+1)).

Lisana juurde veel üks Andrew Ng loengupilt, mis back propagation’t selgitab.

NN disain

Sisendkihis olevate neuronite arv vastab sisendfaktorite arvule. Näiteks kui meil on 28×28 pixslit pilt, siis on sisendneuronite arv 784.

Väljundkihis olevate neuronite arv sõltub, mis tüüpi ülesandega tegu on. Kui me soovime piltidelt tuvastada, kas tegu on autoga või mitte, siis piisa ühest neuronist, mis võtab väärtuse hulgast {0,1}.

Kui ülesanne on klassifitseerida pildid näiteks gruppidesse – autod, inimesed ja majad, siis on mõistlik omada kolme väljund neuronig, mis igaüks eraldi võtab väärtuse hulgast {0,1} e vastuseks on vektorid. Näiteks, kui tegu on NN prognoosib, et sisendpildil on auto, siis väljundvektor oleks [1,0,0], juhul kui tegu on inimesega, siis [0,1,0] ja kui tegu on majaga, siis [0,0,1].

Vahekihte (hidden layers) võib algatuseks valida ühe ja sinna planeeritavate neuronite arv võiks olla sisend+2 või poole suurem. Juhul, kui on vajadus mitme hidden layer’i järele, siis neuroneid igas hidden layer’is peaks olema võrdselt.

NN disain Andrew Ng loengult

Confusion matrix

Posted on August 18, 2015 - August 19, 2015 by margusja

K – Total

P – All positive (TP + TN)

association rules

Posted on August 18, 2015 - August 18, 2015 by margusja

Real life versus designed process

Posted on August 18, 2015 by margusja

Neural network

Posted on August 3, 2015 - August 5, 2015 by margusja

a = x1*w1 + x2*w2 + x3*w3 … xn*wn

Feedforward newwork

In case we have matrix 8X8 we need 64 input

Threshold

Bias

Learning

Learning rate = 0.1
Expected output = 1
Actual output = 0
Error = 1

Weight Update:
w_i = r E x + w_i
w₁ = 0.1 x 1 x 1 + w₁
w₂ = 0.1 x 1 x 1 + w₂

New Weights:
w₁ = 0.4
w₂ = 0.4

Learning rate = 0.1
Expected output = 1
Actual output = 0
Error = 1

Weight Update:
w_i = r E x + w_i
w₁ = 0.1 x 1 x 1 + w₁
w₂ = 0.1 x 1 x 1 + w₂

New Weights:
w₁ = 0.5
w₂ = 0.5

Learning rate = 0.1
Expected output = 1
Actual output = 1
Error = 0

No error,
training complete.

Lets implement it in Java
public class SimpleNN {

private double learning_rate;
private double expected_output;
private double actual_output;
private double error;

public static void main(String[] args) {

// initial
SimpleNN snn = new SimpleNN();
snn.learning_rate = 0.1;
snn.expected_output = 1;
snn.actual_output = 0;
snn.error = 1;

// inputs
int i1 = 1;
int i2 = 1;

// initial weigths
double w1 = 0.3;
double w2 = 0.3;

// loop untill we will get 0 error
while (true) {
System.out.println(“Error: “+ snn.error);
System.out.println(“w1: “+ w1);
System.out.println(“w2: “+ w2);
System.out.println(“actual output: “+ snn.actual_output);
w1 = snn.learning_rate * (snn.expected_output – snn.actual_output) * i1 + w1;
w2 = snn.learning_rate * (snn.expected_output – snn.actual_output) * i2 + w2;
snn.actual_output = w1 + w2;
if (snn.actual_output >= 0.99)
break;
}
System.out.println(“Final weights w1: “+ w1 + ” and w2: “+ w2);

}

Run it:
Error: 1.0
w1: 0.3
w2: 0.3
actual output: 0.0
Error: 1.0
w1: 0.4
w2: 0.4
actual output: 0.8
Error: 1.0
w1: 0.42000000000000004
w2: 0.42000000000000004
actual output: 0.8400000000000001
Error: 1.0
w1: 0.43600000000000005
w2: 0.43600000000000005
actual output: 0.8720000000000001
Error: 1.0
w1: 0.44880000000000003
w2: 0.44880000000000003
actual output: 0.8976000000000001
Error: 1.0
w1: 0.45904
w2: 0.45904
actual output: 0.91808
Error: 1.0
w1: 0.467232
w2: 0.467232
actual output: 0.934464
Error: 1.0
w1: 0.4737856
w2: 0.4737856
actual output: 0.9475712
Error: 1.0
w1: 0.47902848
w2: 0.47902848
actual output: 0.95805696
Error: 1.0
w1: 0.48322278399999996
w2: 0.48322278399999996
actual output: 0.9664455679999999
Error: 1.0
w1: 0.4865782272
w2: 0.4865782272
actual output: 0.9731564544
Error: 1.0
w1: 0.48926258176
w2: 0.48926258176
actual output: 0.97852516352
Error: 1.0
w1: 0.491410065408
w2: 0.491410065408
actual output: 0.982820130816
Error: 1.0
w1: 0.4931280523264
w2: 0.4931280523264
actual output: 0.9862561046528
Error: 1.0
w1: 0.49450244186112
w2: 0.49450244186112
actual output: 0.98900488372224
Final weights w1: 0.495601953488896 and w2: 0.495601953488896

So…Christopher CAN LEARN!!!

Neural network with AND logic.

0 & 0 = 0

0 & 1 = 0

1 & 0 = 0

1 & 1 = 1

Using neural network you can use only one perceptron

In paper calculated weights and AND logic

So we need to find weights fulfil conditions:

0 * w1 + 0 * w2 <= 1

0 * w1 + 1 * w2 <= 1

1 * w1 + 0 * w2 <= 1

1 * w1 + 1 * w2 = 1

Java code to implement this:
public class AndNeuronNet {

private double learning_rate;

private double threshold;

public static void main(String[] args) {

// initial
AndNeuronNet snn = new AndNeuronNet();
snn.learning_rate = 0.1;
snn.threshold = 1;

// AND function Training data
int[][][] trainingData = {
{{0, 0}, {0}},
{{0, 1}, {0}},
{{1, 0}, {0}},
{{1, 1}, {1}},
};

// Init weights
double[] weights = {0.0, 0.0};

snn.threshold = 1;

// loop untill we will get 0 error
while (true) {
int errorCount = 0;

for(int i=0; i < trainingData.length; i++){
System.out.println(“Starting weights: ” + Arrays.toString(weights));
System.out.println(“Inputs: ” + Arrays.toString(trainingData[i][0]));
// Calculate weighted input
double weightedSum = 0;
for(int ii=0; ii < trainingData[i][0].length; ii++) {
weightedSum += trainingData[i][0][ii] * weights[ii];
}
System.out.println(“Weightedsum in training: “+ weightedSum);

// Calculate output
int output = 0;
if(snn.threshold <= weightedSum){
output = 1;
}

System.out.println(“Target output: ” + trainingData[i][1][0] + “, ” + “Actual Output: ” + output);

// Calculate error
int error = trainingData[i][1][0] – output;
System.out.println(“Error: “+error);

// Increase error count for incorrect output
if(error != 0){
errorCount++;
}

// Update weights
for(int ii=0; ii < trainingData[i][0].length; ii++) {
weights[ii] += snn.learning_rate * error * trainingData[i][0][ii];
}

System.out.println(“New weights: ” + Arrays.toString(weights));
System.out.println();
}

System.out.println(“ErrorCount: “+ errorCount);
// If there are no errors, stop
if(errorCount == 0){
System.out.println(“Final weights: ” + Arrays.toString(weights));
System.exit(0);
}

}

Compile and run:

Starting weights: [0.0, 0.0]

Inputs: [0, 0]

Weightedsum in training: 0.0

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.0, 0.0]

Starting weights: [0.0, 0.0]

Inputs: [0, 1]

Weightedsum in training: 0.0

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.0, 0.0]

Starting weights: [0.0, 0.0]

Inputs: [1, 0]

Weightedsum in training: 0.0

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.0, 0.0]

Starting weights: [0.0, 0.0]

Inputs: [1, 1]

Weightedsum in training: 0.0

Target output: 1, Actual Output: 0

Error: 1

New weights: [0.1, 0.1]

ErrorCount: 1

Starting weights: [0.1, 0.1]

Inputs: [0, 0]

Weightedsum in training: 0.0

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.1, 0.1]

Starting weights: [0.1, 0.1]

Inputs: [0, 1]

Weightedsum in training: 0.1

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.1, 0.1]

Starting weights: [0.1, 0.1]

Inputs: [1, 0]

Weightedsum in training: 0.1

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.1, 0.1]

Starting weights: [0.1, 0.1]

Inputs: [1, 1]

Weightedsum in training: 0.2

Target output: 1, Actual Output: 0

Error: 1

New weights: [0.2, 0.2]

ErrorCount: 1

Starting weights: [0.2, 0.2]

Inputs: [0, 0]

Weightedsum in training: 0.0

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.2, 0.2]

Starting weights: [0.2, 0.2]

Inputs: [0, 1]

Weightedsum in training: 0.2

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.2, 0.2]

Starting weights: [0.2, 0.2]

Inputs: [1, 0]

Weightedsum in training: 0.2

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.2, 0.2]

Starting weights: [0.2, 0.2]

Inputs: [1, 1]

Weightedsum in training: 0.4

Target output: 1, Actual Output: 0

Error: 1

New weights: [0.30000000000000004, 0.30000000000000004]

ErrorCount: 1

Starting weights: [0.30000000000000004, 0.30000000000000004]

Inputs: [0, 0]

Weightedsum in training: 0.0

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.30000000000000004, 0.30000000000000004]

Starting weights: [0.30000000000000004, 0.30000000000000004]

Inputs: [0, 1]

Weightedsum in training: 0.30000000000000004

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.30000000000000004, 0.30000000000000004]

Starting weights: [0.30000000000000004, 0.30000000000000004]

Inputs: [1, 0]

Weightedsum in training: 0.30000000000000004

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.30000000000000004, 0.30000000000000004]

Starting weights: [0.30000000000000004, 0.30000000000000004]

Inputs: [1, 1]

Weightedsum in training: 0.6000000000000001

Target output: 1, Actual Output: 0

Error: 1

New weights: [0.4, 0.4]

ErrorCount: 1

Starting weights: [0.4, 0.4]

Inputs: [0, 0]

Weightedsum in training: 0.0

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.4, 0.4]

Starting weights: [0.4, 0.4]

Inputs: [0, 1]

Weightedsum in training: 0.4

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.4, 0.4]

Starting weights: [0.4, 0.4]

Inputs: [1, 0]

Weightedsum in training: 0.4

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.4, 0.4]

Starting weights: [0.4, 0.4]

Inputs: [1, 1]

Weightedsum in training: 0.8

Target output: 1, Actual Output: 0

Error: 1

New weights: [0.5, 0.5]

ErrorCount: 1

Starting weights: [0.5, 0.5]

Inputs: [0, 0]

Weightedsum in training: 0.0

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.5, 0.5]

Starting weights: [0.5, 0.5]

Inputs: [0, 1]

Weightedsum in training: 0.5

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.5, 0.5]

Starting weights: [0.5, 0.5]

Inputs: [1, 0]

Weightedsum in training: 0.5

Target output: 0, Actual Output: 0

Error: 0

New weights: [0.5, 0.5]

Starting weights: [0.5, 0.5]

Inputs: [1, 1]

Weightedsum in training: 1.0

Target output: 1, Actual Output: 1

Error: 0

New weights: [0.5, 0.5]

ErrorCount: 0

Final weights: [0.5, 0.5]

So what we did?

Basically we iterated over the training set until we found good weights to fulfil condition for all records in training set:

if (threshold <= input1[i] * weight1 + input2[i] * weight2) then (if 0 == target[1] done else error and loop again) else (if 1 == target[i] done else error and loop again)

With one perceptor we can solve boolean problems. In picture below you can see weights. Neural network can find them.

Apache-Spark first steps

Posted on June 16, 2015 - June 17, 2015 by margusja

There are two main operations in Spark:

1. Transformations – apply some function to all records in dataset. In example map – mapping input to some new output.

2. Actions – runs some computation and aggregation operation and returns result to driver. In example count and reduce.

Spark’s transformations are lazy. It means if you do not use any action you do not get any results after transformations.

Spark recomputes transformation again before each action. In case you do not want it you can save dataset into memory calling:

> transformationDataSet.persist()

Load data

scala> val data = sc.textFile(“./demo.csv”) // load datafile

var csvData = data.map(l => l.split(“,”).map(_.trim)) // apply split(“,”) to each row in file. Apply trim to each element in row.

inFile.map(x => x.split(‘ ‘)(0)).reduce((a,b) => a)

Here we apply transformation map to each line in inFile dataset. We split each row using ‘ ‘ and take first element. Then we apply action reduce where real staff actually happens due the laziness.

reduce – aggregates elements in dataset using function which takes two arguments and returns one. The function should be commutative and associative so that it can be computed correctly in parallel.

scala> foo
res94: List[Int] = List(1, 2, 3, 4, 5, 6)

scala> foo.reduce((a, b) => a+b)
res95: Int = 21

As I pointed out function have to be associative. In example (1+6)+(2+5)+(3+4)=21 or (2+6)+(1+5)+(3+4)=21

filter (action)

scala> foo
res51: List[Int] = List(1, 2, 3, 4, 5, 6)

scala> foo.filter(x => x > 3)
res52: List[Int] = List(4, 5, 6)

scala> csvData.map(l => l(0).toInt).map(_+1).map(_-1).reduce((a,b) => a+b) // one pointless example how to pipe transfer operations.

Anonymous functions (An anonymous function is a function that is not stored in a program file, but is associated with a variable whose data type is function_handle . Anonymous functions can accept inputs and return outputs, just as standard functions do. However, they can contain only a single executable statement)

scala> val increment = (x: Int) => x + 1

scala> increment(1)
res157: Int = 2

scala> csvData.map(l => l(0).toInt).map(increment(_)).reduce((a,b) => a+b)

scala> val sum2 = (x: Int, y: Int) => x + y

scala> csvData.map(l => l(0).toInt).map(increment(_)).reduce((a,b) => sum2(a,b))