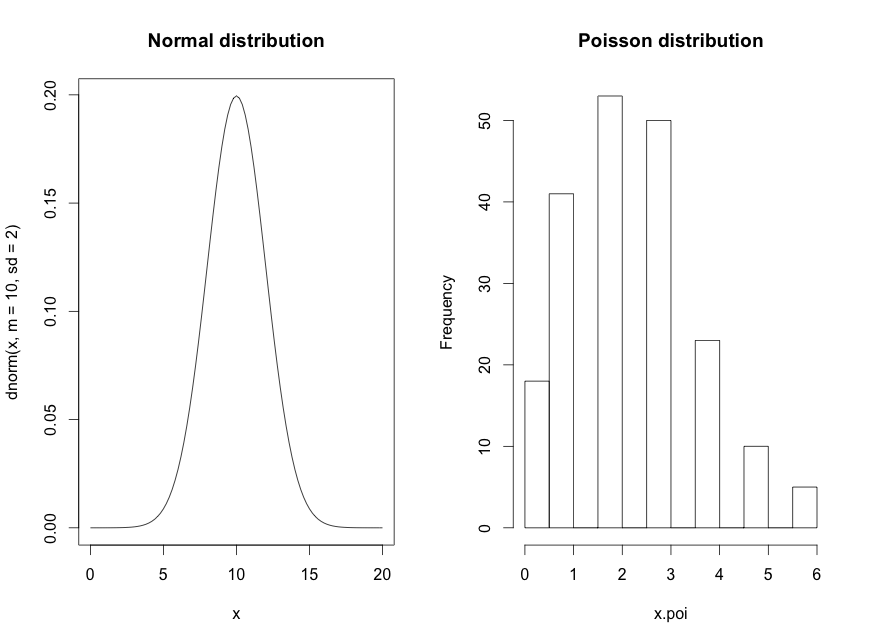
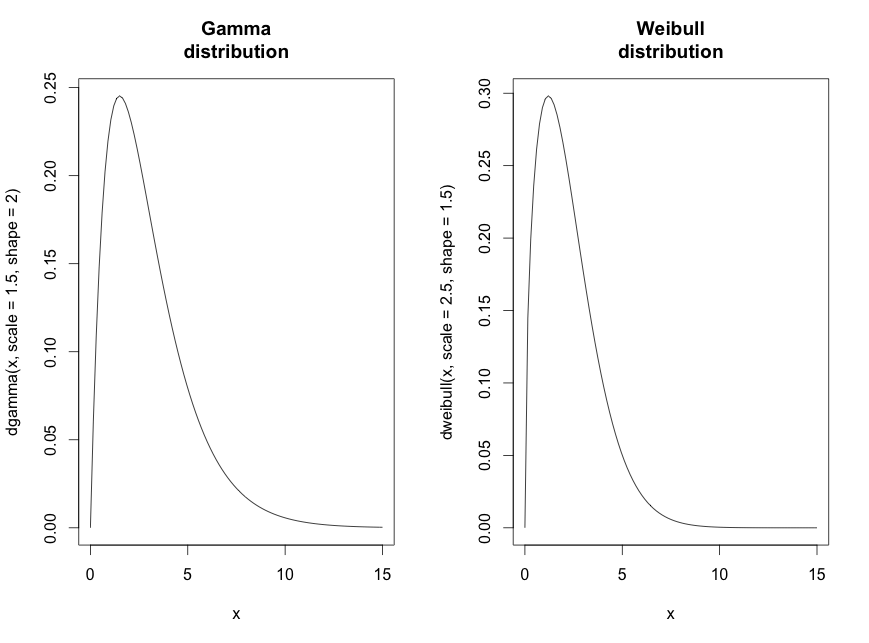
Andmeanalüüsi juures on jaotuste äratundmine väga oluline.
Siinkohal üks võimalus R keskkonnas
Normaaljaotuse puhul on siinkohal andmehulk pidev (loodud x.norm <- rnorm(n=200, m=10, sd=2)) ja Poisson jaotuse puhul on andmehulk diskreetne (loodud x.poi<-rpois(n=200,lambda=2.5)). Gammajaotuse puhul on on tegu pideva andmehulgaga. Genereeritud (dgamma(x, scale=1.5, shape=2)). Weidbulli jaotus on genereeritud dweibull(x, scale=2.5, shape=1.5)
* Teeme illustratiivse näite.
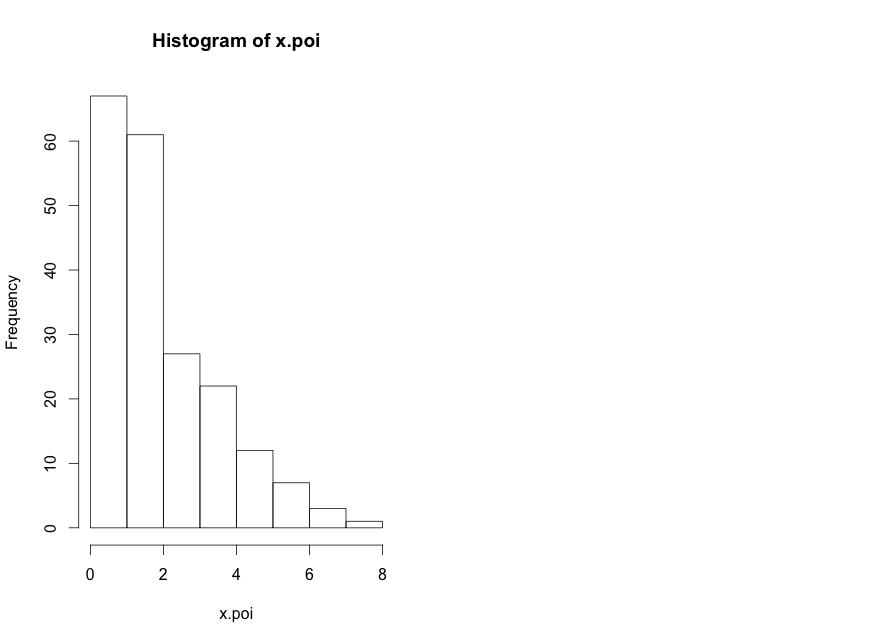
* Loome normaaljaotusega andmehulga x.poi<-rpois(n=200,lambda=2.5)
1 1 2 1 1 2 3 1 1 3 6 1 4 5 4 2 3 5 5 2 1 1 2 2 5 2 1 0 2 4 2 1 2 3 2 3 3 3 2 2 2 3 5 1 2 1 2 1 2 5 4 5 2 3 2 1 1 2 2 5 2 2 1 4 3 1 0 3 3 1 0 1 2 1 2 1 1 1 2 4 0 2 4 2 0 1 2 1 1 1 1 1 6 2 2 3 1 1 0 5 3 1 2 2 2 7 1 4 0 2 1 1 4 3 1 2 1 2 6 3 3 2 2 8 4 5 4 4 1 4 7 2 2 4 0 2 2 1 3 6 7 1 2 2 3 1 2 1 2 3 2 0 4 2 6 1 4 1 4 2 1 2 4 1 3 4 0 3 3 2 2 3 5 1 1 2 2 4 1 2 2 3 3 6 1 1 4 4 1 6 1 1 5 2 1 2 3 2 2 1
* vastav histogramm
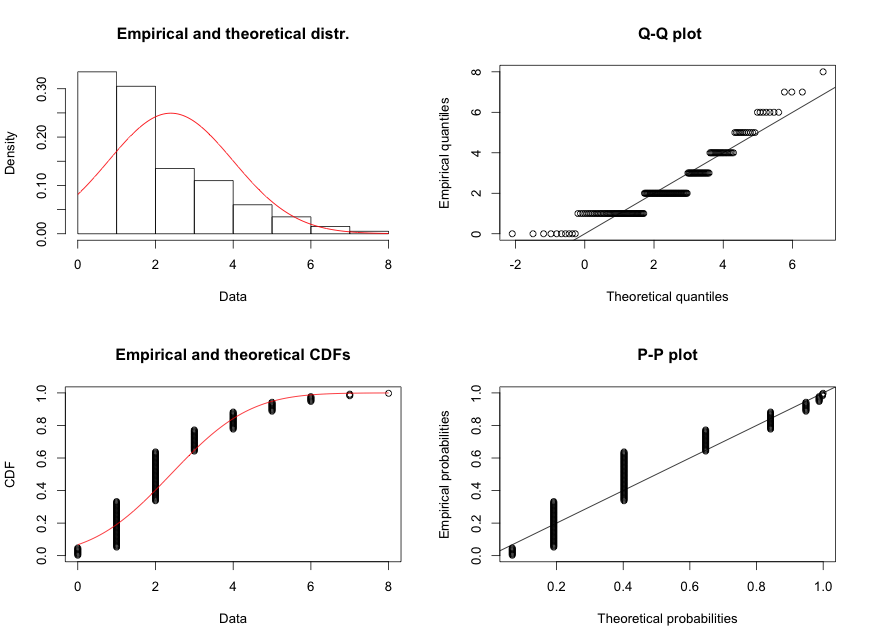
* Kontrollime, milline oleks tulemus, kui me eeldaksime, et tegu oleks normaaljaotusega
Pole just eriti hea.
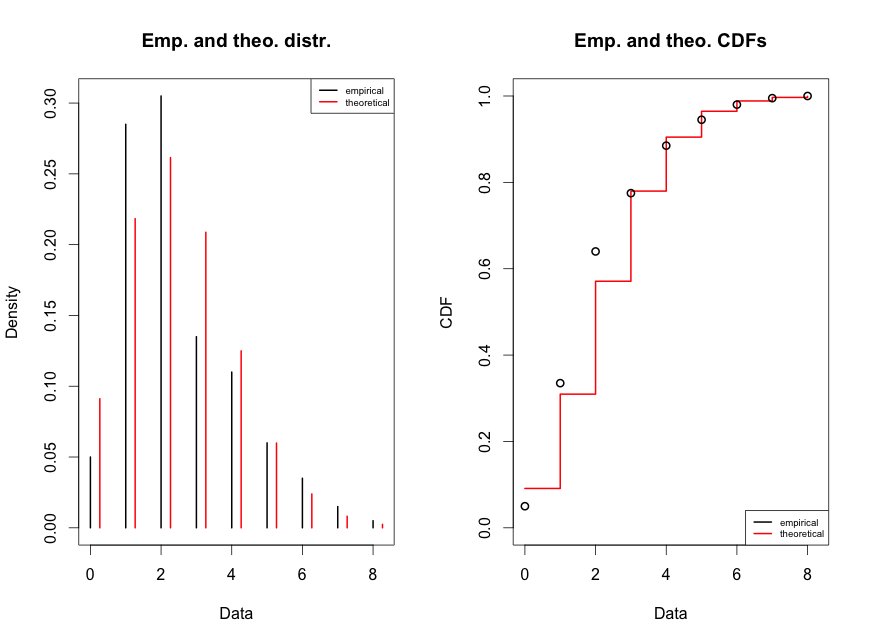
Kontrollime, kui me eeldame, et tegu on Poissoni jaotusega andmehulgaga
Nagu jooniselt näha on, palju parem. Oma andmete jaotusmudeli tundmine on oluline!
Näiteks soovides Pearsoni korrelatsioonikordajat leida Possoni jaotusega andmehulgast, siis ei pruugi see tegevus edasisteks analüüsideks vajaliku infot anda. Teatavasti saab lineaarset korrelatsioonikordajat arvutada noraaljaotusega andmehulga pealt.