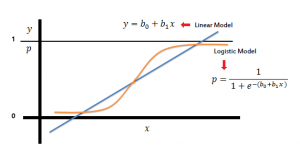
Logistiline regressioon on üks binaarse tunnuse analüüsimeetod, mis prognoosib uuritava sündmuse toimumise tõenäosust ja selle muutumist sõltuvalt pideva argumenttunnuse väärtuse muutumisest
Logistiline regressioon arvutab binaarse tulemuse tõenäosuse ühe või mitme numbrilise ja/või diskreetse faktori põhjal. Lineaarset regressiooni ei saa kasutada binaarse tulemuse tõenäosuse arvutamiseks, kuna tõenäosus ei oleks 0 ja 1 vahel, aga logistiline regressioon tagab, et uuritava sündmuse tõenäosus jääb alati vahemiku 0 kuni 1.
Konstant b0 liigutab logistilise regressioonigraafiku kõverat vasakule ja paremale.
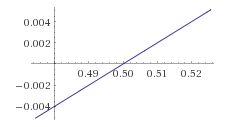
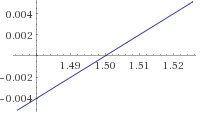
Näiteks lineaarfunktsioon y=-0.1+0.2*x, mille graafik on:
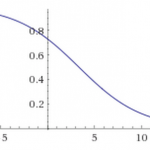
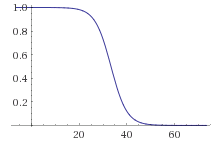
funktsioon 1/(1+e^-(1-0.3*x)) argumendiga b0 = 1, annab graafiku:
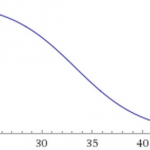
Muutes b0 = 10, annab funktsioon 1/(1+e^-(10-0.3*x)) graafiku:
Muudame konstanti b0 – 0.1 -> 0.3, saame lineaarfunktsiooni y=-0.3+0.2*x, mille graafik on:
Konstant b1…bn mõjutab logistilise regressioonigraafiku kõvera nurka.
funktsioon 1/(1+e^-(10-0.6*x)), kus b1=0.6 graafik on:
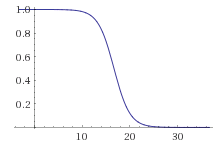
funktsioon 1/(1+e^-(10-0.3*x)), kus b1=0.3 graafik on:
Nagu eelnevalt mainisin, saab logistiline regressioon hakkama suurema hulga parameetritega: 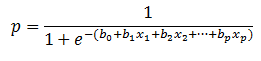
Kindlasti tuleb toonitada, et arvutustulemus annab sündmuse toimumise tõenäosuse, mitte tõenäosus reaalse väärtuse suhtes!
Näiteks andmehulk, kus esimesel kohal on sõltumatu muutuja ja teisel kohal sõltuv muutuja:
X1,Y
18,1
19,1
20,0
20,1
20,1
21,1
25,1
26,0
28,1
32,0
35,0
37,1
37,0
37,0
38,0
40,0
45,0
annab sündmuse toimumise tõenäosused:
X1 Y Calc Prob
18.0000 1 0.8825
19.0000 1 0.8602
20.0000 0 0.8344
20.0000 1 0.8344
20.0000 1 0.8344
21.0000 1 0.8049
25.0000 1 0.6500
26.0000 0 0.6034
28.0000 1 0.5051
32.0000 0 0.3148
35.0000 0 0.2015
37.0000 1 0.1448
37.0000 0 0.1448
37.0000 0 0.1448
38.0000 0 0.1218
40.0000 0 0.0851
45.0000 0 0.0332
Selgelt on näha, et vanuse kasvades, tõenäosus saada Y=1 väheneb.
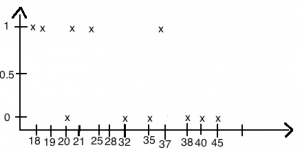
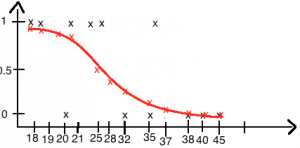
Kanname andmed X/Y koordinaatteljestikule
Proovime ise ka proovimeetodiga leida b0 ja b1 argumente funktsioonile 1/(1+e^-(b0+b1*x))
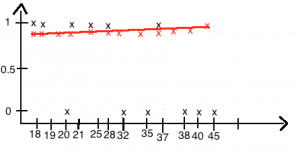
Katsetame b0 = 0.1 ja b1 = 0.1. Saame graafiku:
Antud juhul on kenasti näha, et valitud parameetrid b0 ja b1 ei toimi ja funktsioon ei iseloomusta sõltuvat muutujat peale sõltuva muutuja kasvamist üle 32.
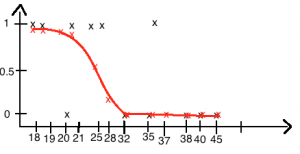
Proovime b0 = 5 ja b1 = -0.2, tulemus on juba reaalsem.
Proovime b0 = 10, b1 = -04, nende parameetrityega oleks tarvis graafikut natukene paremale liigutada.
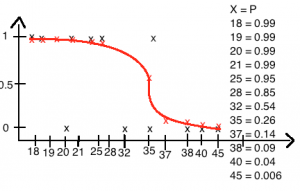
Nagu ma ülal mainisin, saab graafikut paremale ja vasakule liigutada b0 argumendiga.
Valime b0 = 13 ja b1 = -0.4, sest graafiku nn kumerus sobis meile eelmisel katsel. Tulemus on juba ideaalilähedane.
Loomulikult ei tule igapäevases toimimises niimoodi proovimeetodiga kordajaid otsida, samas on ülaltoodu hea selgitus kuidas logistiline regressioon toimib.