Kindlasti on tuttav väljend: “Üks võimalus miljonist.” Erinevad inimesed interpreteerivad eeltoodud lauset omamoodi.
Näiteks, kui ütelda, et lotovõidu tõenäosus on 1:1000 000, siis kas see tähendab, et kui miljon inimest mängib lotot, siis keegi kindlasti võidab? Ei? Tõsi – nii see päris ei ole, kuigi tihti seda nii lahti mõtestatakse. Aga kuidas suhet 1:1000 000 siis mõista?
Seletamiseks võtame natukene lihtsama skaala – täringu. Küsime: “Kui tõenäoline on, et kuue viske jooksul ei saa me kordagi kuut silma?” Arvutatakse seda järgnevalt: (1-(1/6))^6 e 1/6 on tõenäosus, et visatakse kuus iga eraldi katse käigus. 1- on vastassündmuse jaoks. Astendaja kuus on katsete arv. Selgub, et antud arvutuse tulemus on ligikaudu 0.33 e 1/3 on tõenäosus, et kuue viske jooksu ei tule kordagi kuus. Võis siis 2/3 on tõenäosus, et tuleb kuus.
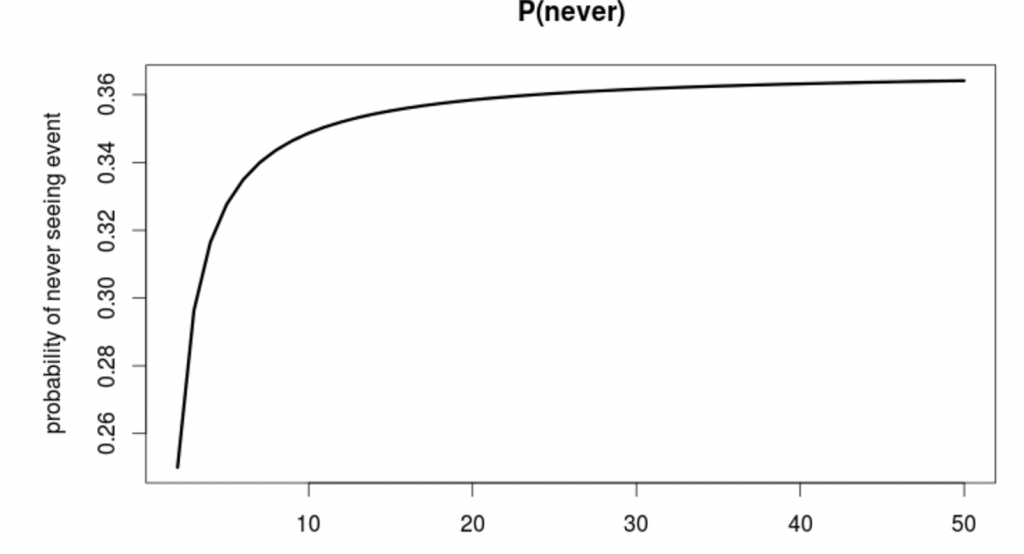
Ülaltoodust saab üsna lihtsalt tuletada üldvalemi – P(newer) = (1-(1/n))^n
Kui nüüd antud funktsiooni kuju vaadata (Joonis 1.), siis selgub, et tõenäosus katsete arvu suurenemisel praktiliselt ei suurene e võib ka väita, et miljoni viskamise korral ei saa väga kindlalt väita, et kuus ikka tuleb.
Joonis 1.
Mis aga kõige lahedam. Aastal 1690 J. Bernoulli tegeles sama probleemiga ja avastas, et katsete väga suurel hulgal allub graafik palju lihtsamale valemile – 1/e
Allikas: https://www.countbayesie.com/blog/2015/2/18/one-in-a-million-and-e