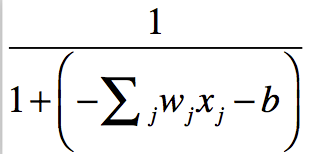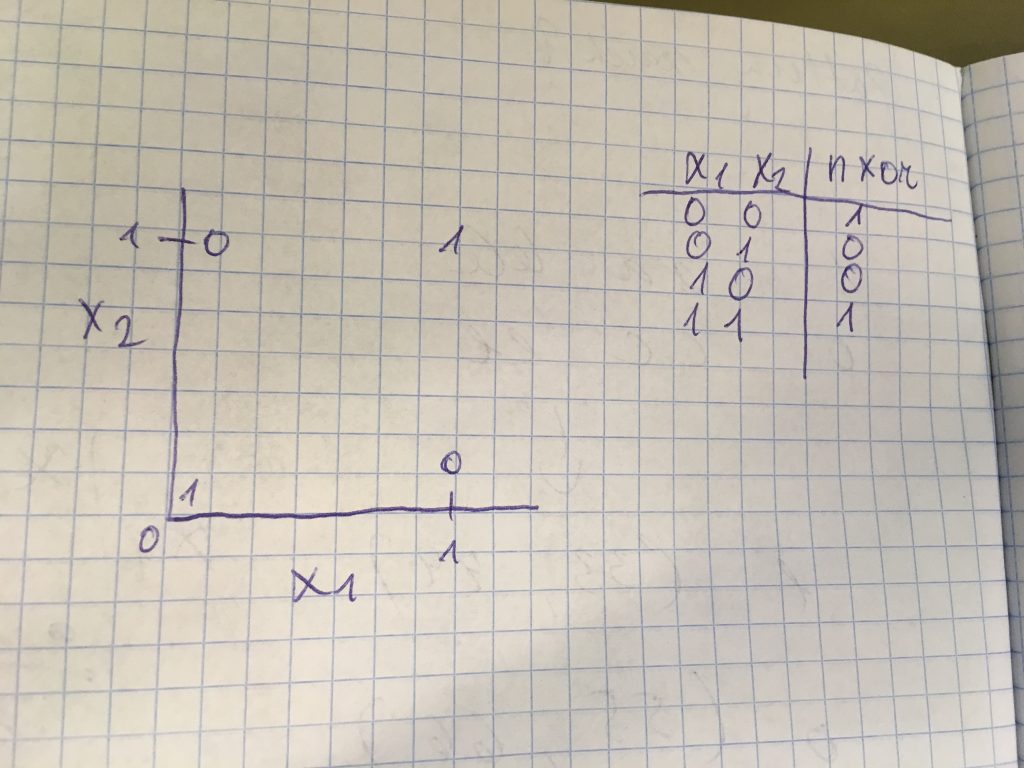Kuna arvutusvõimsus on sealmaal, et närvivõrgustiku analoogial välja töötatud tehnoloogia on nüüdseks kasutatav, siis teen enda jaoks taas asja puust ja punaselt ette. Noh, et oleks võtta juhul kui keegi küsib ja jube tark paistan ka välja.
Neuron Network ja Deep Learning on selline tehnoloogia, et väidetavalt saab nende abil lahendada suvalist pidevat funktsiooni. Tingimuseks on vaid piisav arv neuroneid ja hidden layereid. Kõlab paljulubavalt. Seega tasub sellel tehnoloogial silma peal hoida.
Et anda aimu neuron network toimimisest, defineerin lihtsa ülesande. Oletame, et mul on andmetabel kahest sisendist ja väljund.
0 ja 0 annab 0
0 ja 1 annab 0
1 ja 0 annab 1
1 ja 1 annab 1
ehk kaks sisendit ja üks väljund.
Sellise masina ehitamine, mis ülaltoodut realiseeriks oleks kindlasti lihtsam ehitada mõne teise tehnoloogiaga, aga siinkohal sobib antud ülesanne oma lihtsuse tõttu neuron network’i põhimõtet demonstreerima.
Neuron network kontekstis nimetatakse sisendeid ja väljundeid leieriteks (leyer ik.).
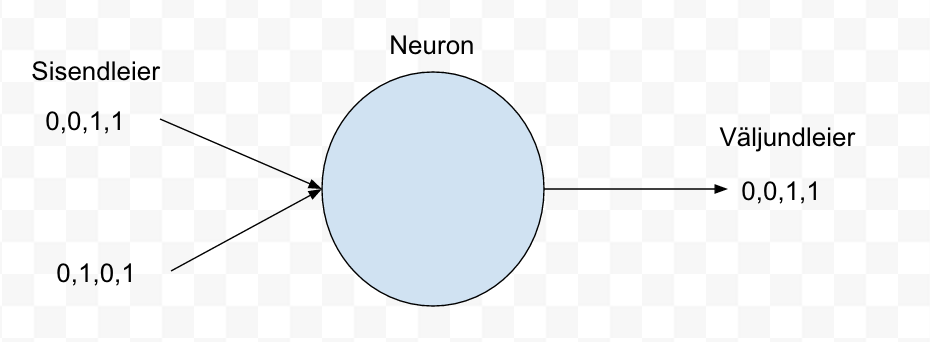
Meie sisendleieriks on paarid o,o ; 0,1 ; 1,0 ; 1,1 ja vastavateks väljundleieriteks 0, 0, 1, 1
Kuna on soov ehitada väga lihtne neuron networks, siis lihtsaim, mida ehitada saab on ühe neuroniga võrk (perceptron). Vt joonis 1.
Joonis 1
Üks neuron network’i põhiomadusi on adapteeruda ehk vigadest õppida. Kui me mõnda aega oleme ütelnud oma neuron network’le, et sisend 0,0 ei ole mitte 1 vaid 0, siis lõpuks saab ta sellest aru. Kuidas?
Iga leieri ja neuroni vahel olev ühendus nn kaalutakse. Harilikult vahemikus -1 kuni 1.
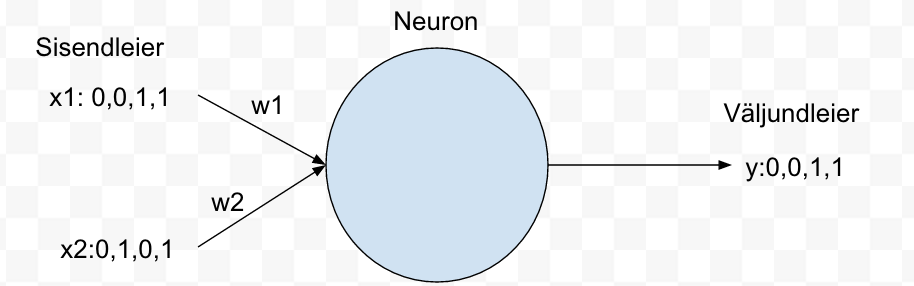
Joonisel 2 oleme lisanud ka kaalud w1 ja w2. Ühtlasi tähistasime ka sisendid x1 ja x2 ja väljundi y.
Joonis 2
Nüüd läheme neuroni kallale. Neuron teeb mingi tehte sisenditega ja kaaludega. Võrdleb arvutatud väljundit tegeliku väljundiga. Arvutab vea ja muudab vastavalt saadud veale kaalusid ja alustab otsast peale. Niikaua kuni viga on piisavalt väike e arvutatud väljund on piisavalt sarnane tegelikule väljundile.
Oluline on leida kaalud (w1,w2,w3), mis sobivad kõikide sisendi paaride korral.
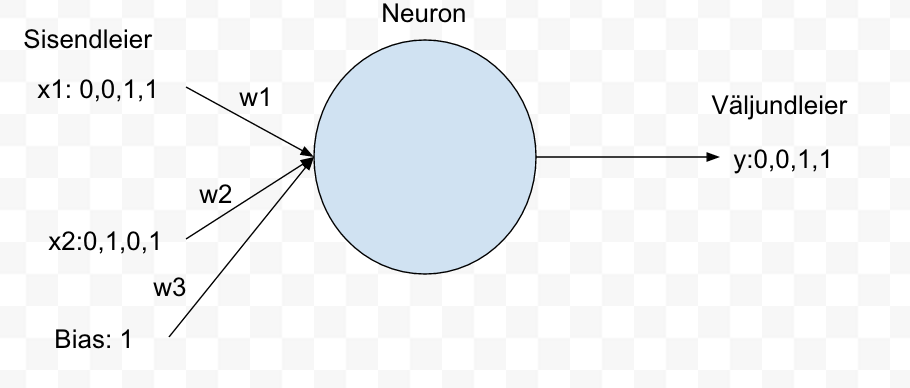
Sisendite hulka on lisatud ka bias. Bias on üks võimalusi määrata kui tundlik on väljund. Mida suurem on bias seda lihtsam on neuronil võimalik aktiveeruda. Antud näite juures valime bias=1. Vt joonis 3.
Joonis 3
NB! Juhul kui realiseerida NN programmatiliselt ise, siis peab tähelepanu pöörama asjaolule, et ei valitaks alustamiseks kõike kaalusid näiteks 0 väärtusega või sarnaseid. Sobivad juhuslikud väärtused 0 ja 1 vahel.
Meie lihtne neuron omab arvutust:
algus:
- w1 ja w2 = mingid suvalised kaalud vahemikus -1 kuni 1
- y=(x1*w1)+(x2*w2)+(bias*w3)
- error = õige vastus – y
- Kui viga on liiga suur:
- w1 = w1+error*x1
- w2 = w2+error*x2
- siis mine tagasi algusesse
lõpp;
Lihtsa programmi abil võin kinnitada, et peale tuhandet iteratsiooni on mul kaalud, mis sobivad iga paari jaoks.
w1:9.67299303, w2:-0.2078435, w3:-4.62963669
Proovime neid:
Paar 0,0:
- (0*9.67299303)+(0*-0.2078435)+(1*-4.62963669)=-4,62963669
Paar 0,1
- (0*9.67299303)+(1*-0.2078435)+(1*-4.62963669)=-4,83748019
Paar 1,0
- (1*9.67299303)+(0*-0.2078435)+(1*-4.62963669)=5,04335634
Paar 1,1
- (1*9.67299303)+(1*-0.2078435)+(1*-4.62963669)=4,83551284
Tulemus pole just see, mida ootasime? Nüüd tuleb mängu viimane element neuron network’is – activation function, mis kuulub iga neuroni juurde. Nagu ülalt näha, siis võime kirjeldada kolmikud:
0,0,-4.62963669
0,1,-4.83748019
1,0,5.04335634
1,1,4.83551284
Kui me nüüd laseme kolmikute viimase elemendi läbi lihtsa funktsiooni:
activationFunction (x):
Kui x <= 0 siis väljund 0
muidu väljund 1
end:
0,0,activationFunction(-4.62963669)
0,1,activationFunction(-4.83748019)
1,0,5,activationFunction(5.04335634)
1,1,activationFunction(4.83551284)
teisisõnu:
0,0,0
0,1,0
1,0,1
1,1,1
Kui nüüd selliseid ninaarseid tehteid teostavaid neoroneid omavahel kombineerida, siis saab lahendada suvalise loogikafunktsiooni.
Vot selline tubli loom on see neuron network. Masinad õpivad 🙂
Üleval käsitlesin “perceptron”i ehk sisendiks on 1 või null ja väljund on 0 kui (X1*W1)+(X2*W2)+b <=0 ja väljund on 1 kui (X1*W1)+(X2*W2)+b > 1
Sigmoid neuron
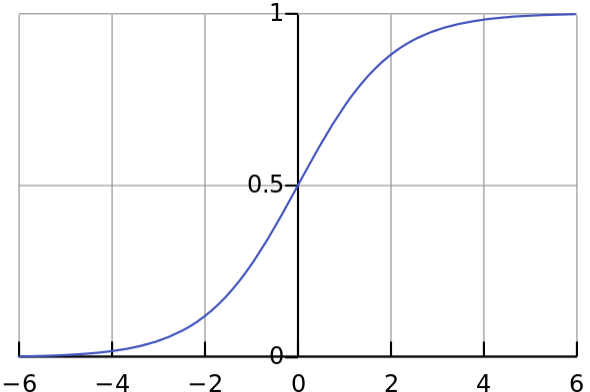
Sarnaneb perceptron’le aga sisendid on 0 ja 1 vahel reaalarvud ja väljundiks on sigmoid funktsioon:
Lihtne näide (mida saab palju lihtsamalt lahendada, aga antud kontekstis siiski ilmekas) on NXOR. Selge on see, et lineaarse funktsiooniga ei ole siin midagi peale hakata.
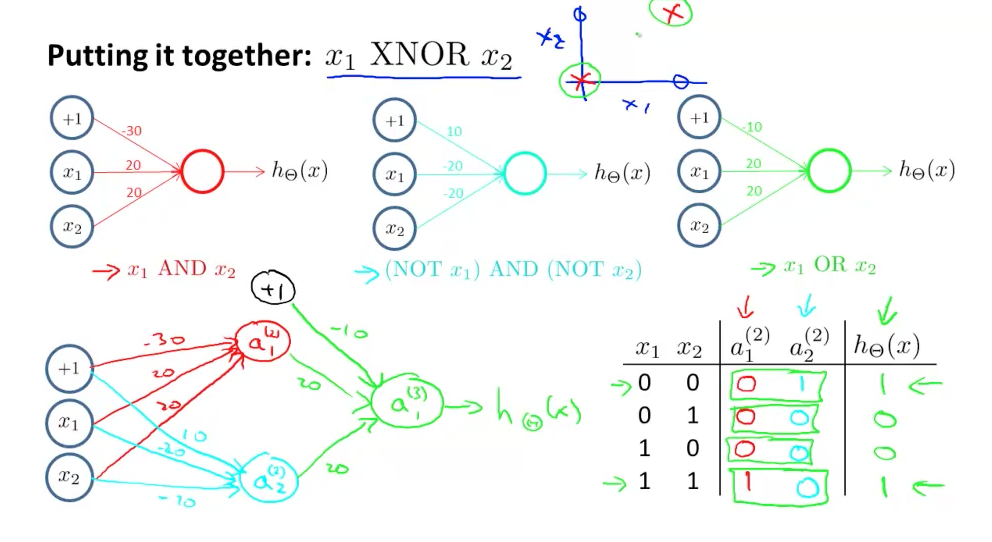
Siinkohal toon ühe pildi Andrew Ng loengust, kus on näha, kuidas erinevaid binaarseid tehteid kombineerida ning saavutada mittelineaarne väljund.
Allpool on näha, et meil on kaks neuronit hidden kihis, mis realiseerivad erinevaid funktsioone ja mille väljundit tarbib väljundkiht, mis realiseerib mittelineaarse funktsiooni.
Back Propagation
Minu jaoks suht keeruline teema, aga paari sõnaga kuidas mina asjast aru saan.
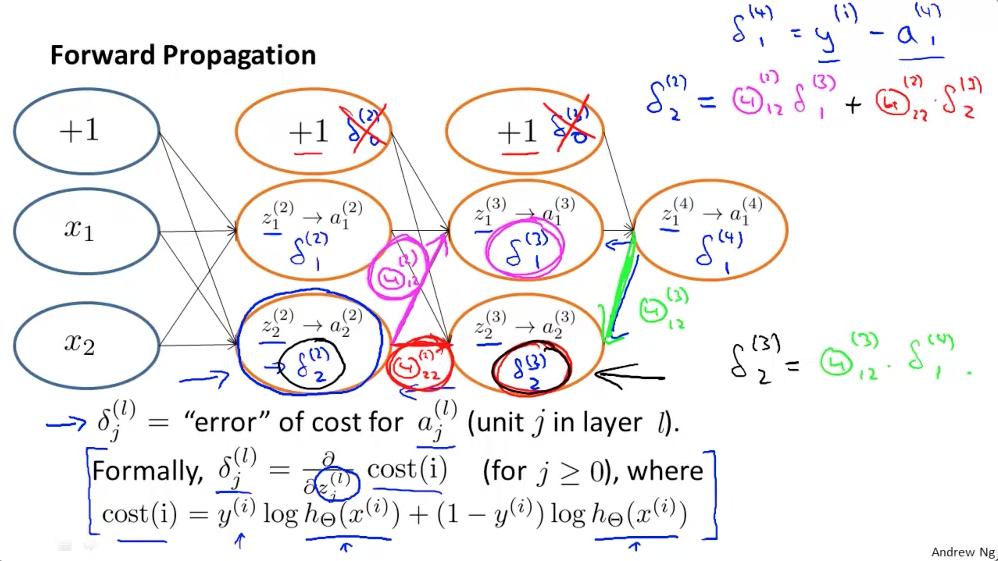
Kui Forward Propagation on eelmisest (vasakul asuvast) kihist tulevate aktiveerimis funktsioonide väärtuste ja kaalude korrutiste summa -Ai( Sum(A(i-1)*W(i-1))) kus i tähistab aktiivset kihti, siis back propagation puhul on tegu järgnevasse (paremale) kihti suunatud kaalude ja järgneva (parema) kihi cost funktsiooni tulemuste korrutiste summa – Sum(W(i+1)* (Di+1)).
Lisana juurde veel üks Andrew Ng loengupilt, mis back propagation’t selgitab.
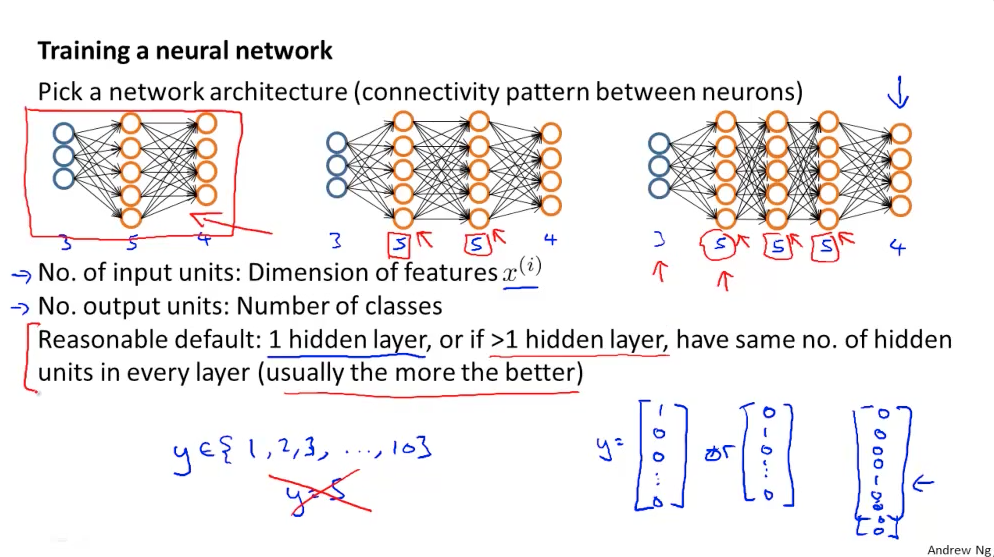
NN disain
Sisendkihis olevate neuronite arv vastab sisendfaktorite arvule. Näiteks kui meil on 28×28 pixslit pilt, siis on sisendneuronite arv 784.
Väljundkihis olevate neuronite arv sõltub, mis tüüpi ülesandega tegu on. Kui me soovime piltidelt tuvastada, kas tegu on autoga või mitte, siis piisa ühest neuronist, mis võtab väärtuse hulgast {0,1}.
Kui ülesanne on klassifitseerida pildid näiteks gruppidesse – autod, inimesed ja majad, siis on mõistlik omada kolme väljund neuronig, mis igaüks eraldi võtab väärtuse hulgast {0,1} e vastuseks on vektorid. Näiteks, kui tegu on NN prognoosib, et sisendpildil on auto, siis väljundvektor oleks [1,0,0], juhul kui tegu on inimesega, siis [0,1,0] ja kui tegu on majaga, siis [0,0,1].
Vahekihte (hidden layers) võib algatuseks valida ühe ja sinna planeeritavate neuronite arv võiks olla sisend+2 või poole suurem. Juhul, kui on vajadus mitme hidden layer’i järele, siis neuroneid igas hidden layer’is peaks olema võrdselt.
NN disain Andrew Ng loengult