Binoomjaotus
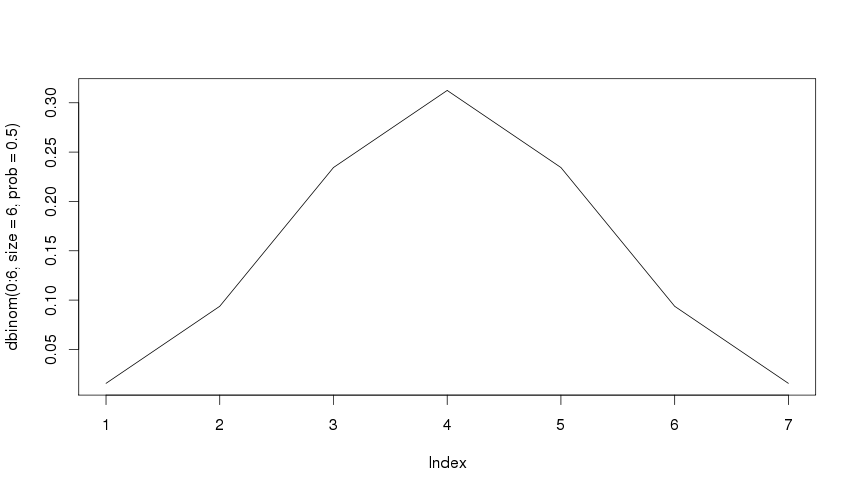
P(X=x) Oletame, et me viskame kulli ja kirja. Lihtsuse mõttes eeldame, et kulli ja kirja tulemise tõenäosus on 1/2 ehk 0.5. Kuigi kui päris aus olla, siis peaks see olema 0.3. Mis on tõenäosus, et me kuuest viskest ei saa ühtegi kulli? R keskkinnas aitab meid tihedusfunktsioon
> dbinom(0:6, size=6, prob=0.5)
[1] 0.015625 0.093750 0.234375 0.312500 0.234375 0.093750 0.015625
ehk visete arv on kuus (size=6), sündmuse esile tulemise tõenäosus 0.5 (prob) Vastusest loeme, et Võimalus, et me kordagi kulli ei viska on 0.015625 ehk väga väike võimalus. Võimalus, et me viskame kulli kolmel korral on 0.312500 Võimalus, et meil veab ja me viskame kulli kuuest korral kuus on 0.015625 - samuti väga väike. Graafik, mis meie juttu visualiseerib. X telg algab tegelikult 0 mitte 1...7 vaid loe 0...6
P(X<=x)
Teeme teise viskamiste seeria veel. Viskan veelkord kulli kuus korda ja nüüd tahan teada, et mis on tõenäosus, et kull tuleb 6 või vähem korda?
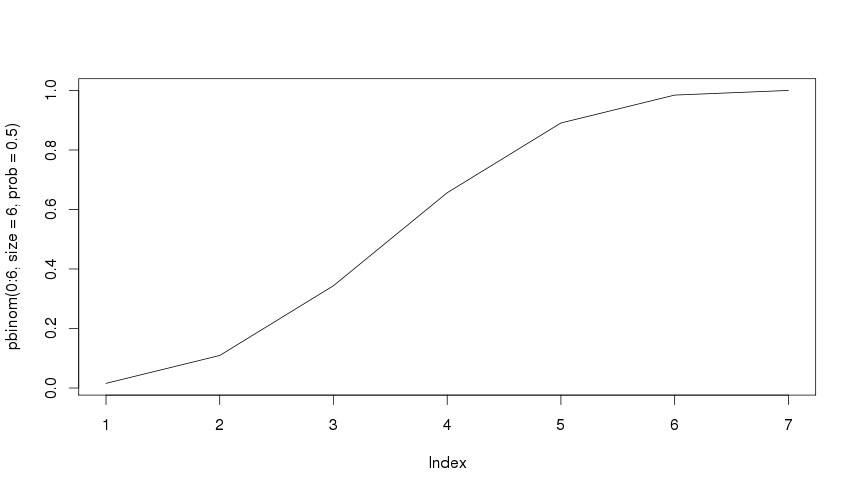
R keskkonnas aitab meid jaotusfunktsioon
> pbinom(0:6, size=6, prob=0.5) [1] 0.015625 0.109375 0.343750 0.656250 0.890625 0.984375 1.000000
Siit võime välja lugeda, et tõenäosus visata kuuel korral kuus kulli või alla selle on päris suur - 100%. Kõlab loogiliselt. Samas nagu näha on visata näiteks kuuel korral viis või vähem korda kulli on juba 98% tõenäosus. Ja visata kuuel viskel ainult korra või mitte ühtegi korda kulli on 1%.
Graafik, mis meie juttu visualiseerib