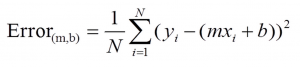Linear regression with one independent variable is easy. It is easy to us for humans. But how machine knows what is the best line thru points? Math helps again!
In example lets take very trivial dataset in python:
points = [ [1,1], [2,2], [3,3], [4,4], [5,5], [6,6], [7,7], [8,8], [9,9] ]
And some lines of python code
a_old = 34 # random initial value
a_new = -2 # random initial value
b_old = 34 # random initial value
b_new = 3 # random initial value
learningRate = 0.01 # step size
precision = 0.00001
while abs((a_new – a_old)-(b_new – b_old) ) > precision:
ret = stepGradient(b_new, a_new, points, learningRate)
a_old = a_new
b_new = ret[0]
b_old = b_new
a_new = ret[1]
print ret[0]
print ret[1]
print “—-“
And stepGradient code is behind gradient descent formula
def stepGradient(b_current, a_current, points, learningRate):
b_gradient = 0
a_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
b_gradient += -(2/N) * (points[i][0] – ((a_current*points[i][1]) + b_current))
a_gradient += -(2/N) * points[i][1] * (points[i][0] – ((a_current * points[i][1]) + b_current))
new_b = b_current – (learningRate * b_gradient)
new_a = a_current – (learningRate * a_gradient)
return [new_b, new_a]
After running our code, at least in my computer the last two rows are:
0.0152521614476
0.997576043517
So the first one is basically 0 and the last one in 1 – pretty perfect in our case.