Category: Linux
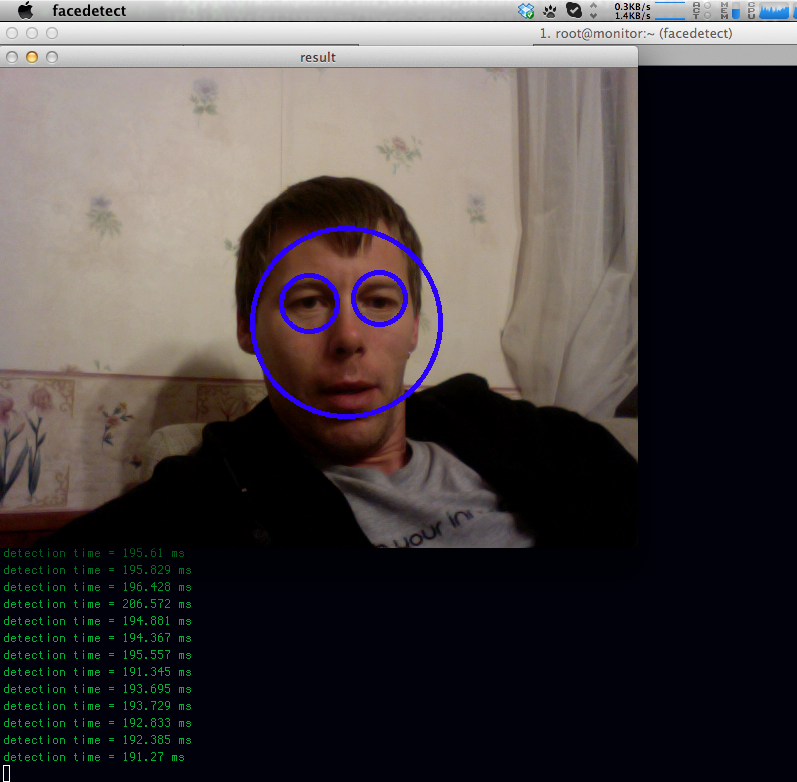
OpenCV and facedetection
I got it work đ
Mac OS X avrdude Atmel AVR ISP mkII TMEGA328P
ISP 6-way pinout
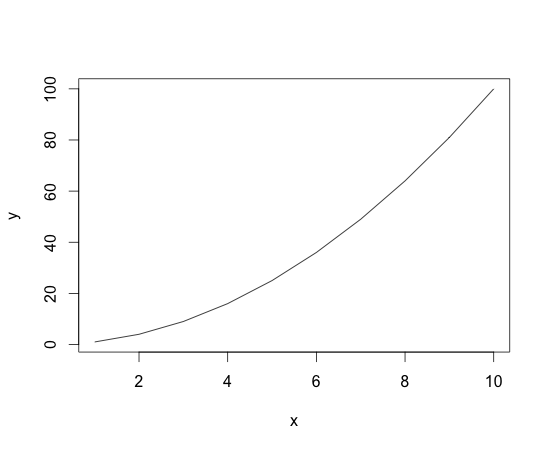
R and lm summary output
> c
x y
1 1 1
2 2 4
3 3 9
4 4 16
5 5 25
6 6 36
7 7 49
8 8 64
9 9 81
10 10 100
> summary(fitted.regression)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-8 -6 -2 4 12
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -22.0000 5.5498 -3.964 0.00415 **         # Kasutades Coefficients Estimate -22.0000 + 11.0000 * x saame antud mudeli (fitted.regression) pÔhjal ennustatava y vÀÀrtuse. Vabaliige -22.0000 kui x on 0 siis y = -22.0000
x           11.0000 0.8944 12.298 1.78e-06 ***       #  Estimate/Std. Error=t value (11.0000/0.8944=12.29875 – standard errors away from zero) Kui t value on suurem kui 3, siis on vĂ€ga suur tĂ”enĂ€osus, et x on seotud y-ga.
—
Signif. codes: 0 â***â 0.001 â**â 0.01 â*â 0.05 â.â 0.1 â â 1
Residual standard error: 8.124 on 8 degrees of freedom  # Residual standard error: 8.124 = sqrt(mean(residuals(fitted.regression) ^ 2)) – kuigi antud juhul saan mina 7.266361Â
Multiple R-squared: 0.9498, Adjusted R-squared: 0.9435 # Multiple R-squared: 0.9498 kui suurt osa x-st kasutati andmetest meie mudeli koostamisel. 0.9498 -> 94% on vÀga hea
F-statistic: 151.3 on 1 and 8 DF, p-value: 1.778e-06
> -22.0000 + 11.0000 * 1
[1] -11
> -22.0000 + 11.0000 * 2
[1] 0
> -22.0000 + 11.0000 * 3
[1] 11
> -22.0000 + 11.0000 * 4
[1] 22
> -22.0000 + 11.0000 * 5
[1] 33
> -22.0000 + 11.0000 * 6
[1] 44
> -22.0000 + 11.0000 * 7
[1] 55
> -22.0000 + 11.0000 * 8
[1] 66
> -22.0000 + 11.0000 * 9
[1] 77
> -22.0000 + 11.0000 * 20
[1] 198
> -22.0000 + 11.0000 * 100
[1] 1078
SME – squared mean error
Meil on andmehulk kus on 100 rida ja kaks veergu – suitsetab (1/0) ja vanus millal uuritav suri:
1 – 68
0 – 70
jne…
Kogu andmehulga pealt vanuse keskmine on – 72.723
Suitsetajate keskmine vanus antud andmehulgas on 70.192
Mittesuitsetajate keskmine vanus antud andmehulgas on 75.254 (Suitsetamine tÔesti rikub tervist)
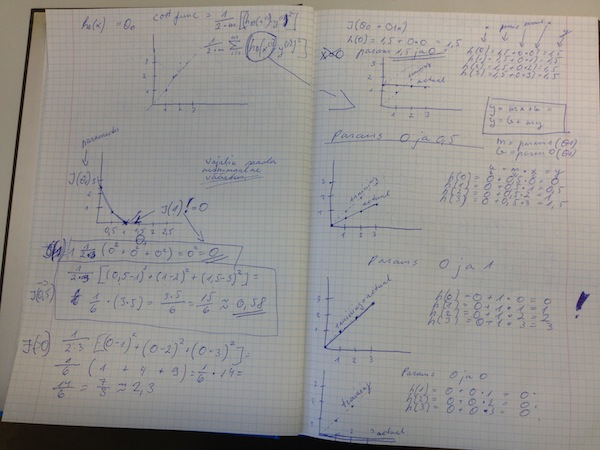
Antud andmehulk on lihtne, kui proovida ennustada keskmist eluiga SME valemiga mean((y – h) ^ 2) kus y on vektor, mis sisaldab vanuseid, siis saame vastuseks vÀÀrtuse, mis vĂ€ljendab y asukohta x teljest.
Kui nĂŒĂŒd antud andmehulga pealt teha see arvestus siis saame vastuseks 32.991, mis ongi squared mean error.
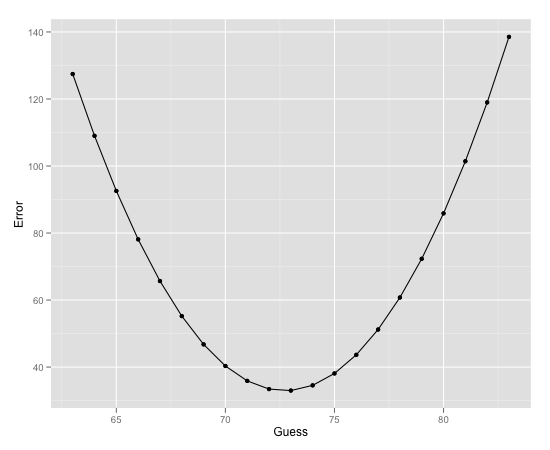
Kuna tegu on ruutfunktsiooniga, siis on seda kerge ka visualiseerida –
VĂ”tame hĂŒpoteesid (vanused, mis vĂ”iksid olla antud andmehulga pĂ”hjal keskmised), mida me proovime:
63 – 127.451
64 – 109.005
65 – 92.559
66 – 78.113
67 – 65.667
68 – 55.221
69 – 46.775
70 – 40.329
71 – 35.883
72 – 33.437
73 – 32.991
74 – 34.545
75 – 38.099
76 – 43.653
77 – 51.207
78 – 60.761
79 – 72.315
80 – 85.869
81 – 101.423
82 – 118.977
83 – 138.531
Ja moodustame graafiku:
Kuna antud andmehulk on lihtne, siis SME ja keskmine antud vektorist langevad suhteliselt kokku
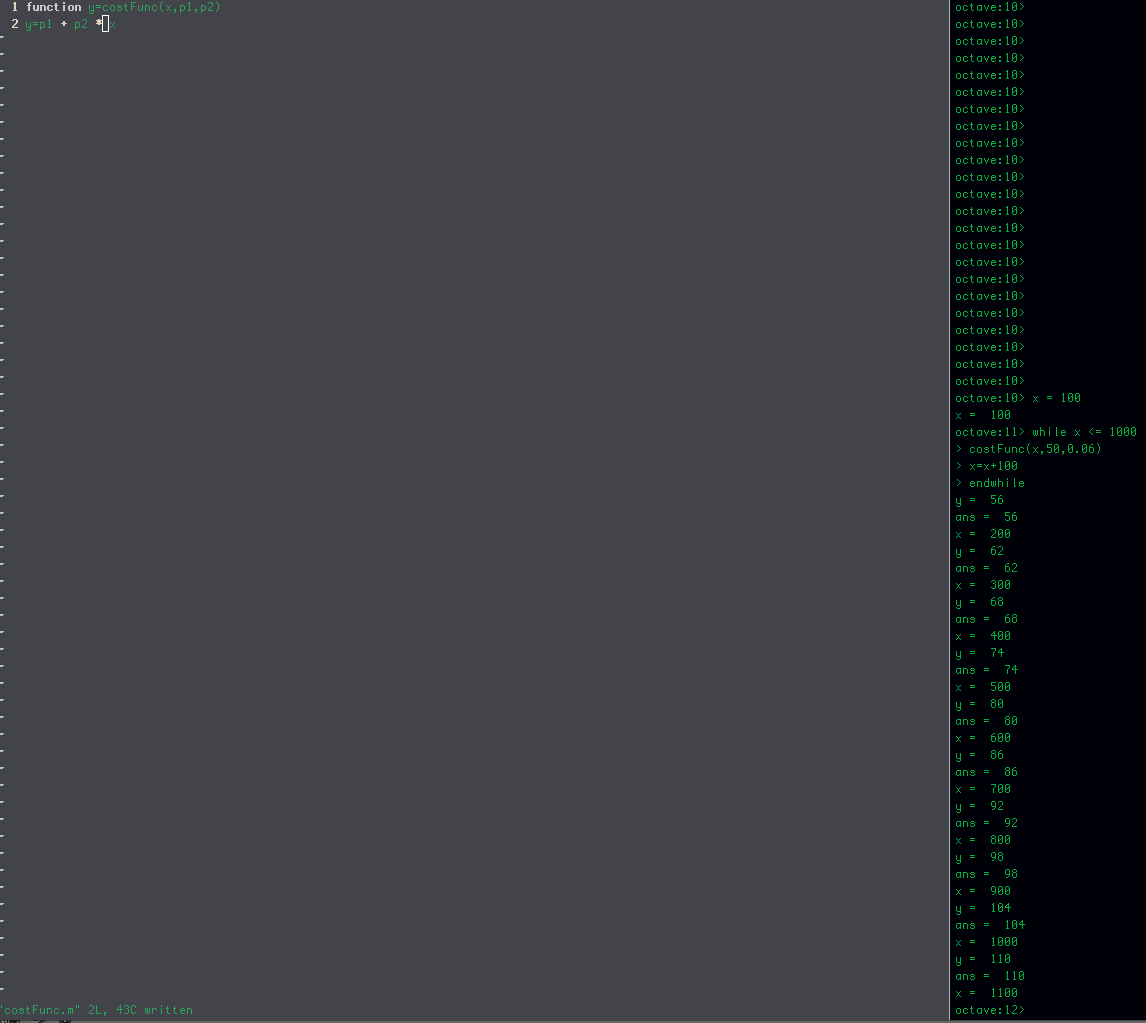
Linear regression and cost function with octave
TööpÀev ja tulemus
Lihtne temperatuuri ja niiskuse mÔÔdik
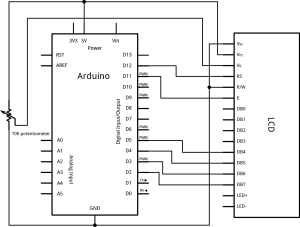
Komponendid:
Arduino Uno komplekt
SHT10
LCD display
10K takisti
Kasutasin SHT1x lib for arduino https://github.com/practicalarduino/SHT1x ja arduino LCD lib http://arduino.cc/en/Tutorial/LiquidCrystal.
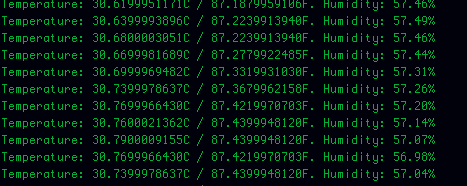
Esmalt ĂŒhendasin SHT10 ja kontrollisin kas andmed on mĂ”istlikud – ei olnud. Peale 10K pull up takisti paigaldamist sain rahuldavad andmed.
NĂŒĂŒd ĂŒhendasin LDC display ja lisasin koodile LDC lib ja vastavad read, et info jĂ”uaks LCD display peale.
Kogu kupatus sai selline pusa
Ja tulemus siin
Edasise arengu huvides tĂ”stsin kivi eraldi, ei saa ju iga lĂ”pplahenduse jaoks tervet arduino konstruktorit vĂ”tta đ
Edasi sai vormistatud natukene robustselt eraldi plaadile.
Vectorization is simple ;)
