> summary(fit)
Call:
lm(formula = mydata$mpg ~ mydata$cyl, data = mydata) // Mudel, mida kasutati
Residuals:
Min 1Q Median 3Q Max
-4.9814 -2.1185 0.2217 1.0717 7.5186 // Punkthinnangud
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 37.8846 2.0738 18.27 < 2e-16 *** // a
mydata$cyl -2.8758 0.3224 -8.92 6.11e-10 *** // sõltumatu muutuja korrutis – b
Estimated – Funktsiooni ennustatud koefitsendid, lineaarse regressiooni korral (y=bx+a) a ja b.
Std. Error –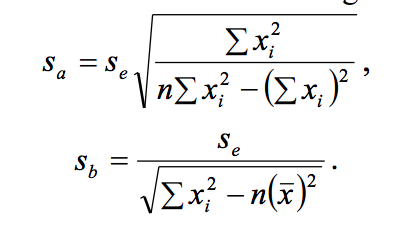
// (t value korrelatsiooni põhjal arvutatud statistiku empiiriline väärtus)
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1 – alla 0.05 on statistiliselt olulised regressioonivõrrandis.
Residual standard error: 3.206 on 30 degrees of freedom
Multiple R-squared: 0.7262, Adjusted R-squared: 0.7171 // Determinatsioonikordaja – regressioonimudeli suutlikus kirjeldada mõõdetud suurusi skaalal 0 kuni 1.
F-statistic: 79.56 on 1 and 30 DF, p-value: 6.113e-10
p-value – Eksimuse tõenäosus sisukat (Enamasti H1) hüpoteesi eelistades. Mida väiksem, seda väiksem on eksimise tõenäosus. Harilikult alla 0.05 oleks soovitatav.
> mydata
mpg cyl
Mazda RX4 21.0 6
Mazda RX4 Wag 21.0 6
Datsun 710 22.8 4
Hornet 4 Drive 21.4 6
Hornet Sportabout 18.7 8
Valiant 18.1 6
Duster 360 14.3 8
Merc 240D 24.4 4
Merc 230 22.8 4
Merc 280 19.2 6
Merc 280C 17.8 6
Merc 450SE 16.4 8
Merc 450SL 17.3 8
Merc 450SLC 15.2 8
Cadillac Fleetwood 10.4 8
Lincoln Continental 10.4 8
Chrysler Imperial 14.7 8
Fiat 128 32.4 4
Honda Civic 30.4 4
Toyota Corolla 33.9 4
Toyota Corona 21.5 4
Dodge Challenger 15.5 8
AMC Javelin 15.2 8
Camaro Z28 13.3 8
Pontiac Firebird 19.2 8
Fiat X1-9 27.3 4
Porsche 914-2 26.0 4
Lotus Europa 30.4 4
Ford Pantera L 15.8 8
Ferrari Dino 19.7 6
Maserati Bora 15.0 8
Volvo 142E 21.4 4
> chisq.test(mydata)
Pearson’s Chi-squared test
data: mydata
X-squared = 46.1698, df = 31, p-value = 0.03908
Oletame, et me oleme võtnud eesmärgiks tõestada, et kahe tulba vahel (mpg ja cyl) on seos, siis H1 e alternatiivne hüpotees oleks, et kahe tulba vahel on seos ja Ho on, et seos puudub.
Kuna p-value on 0.03 e väiksem, kui 0.05, siis võime 5% eksimismääraga vastu võtta H1 hüpoteesi.