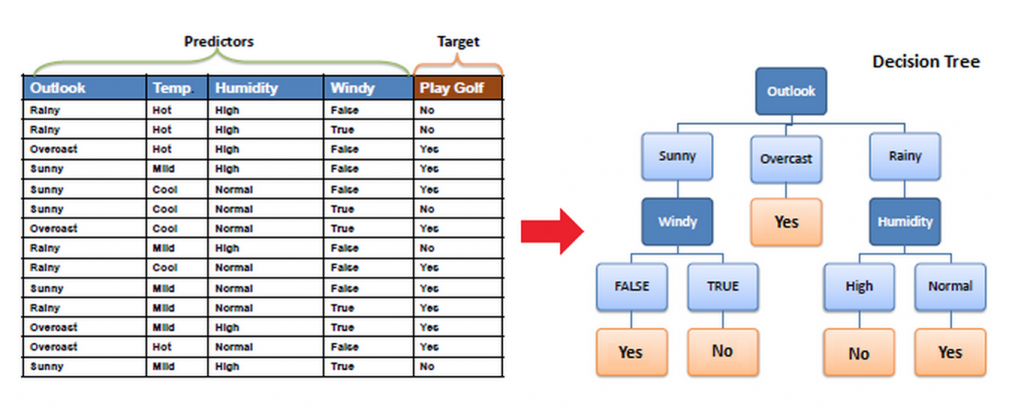
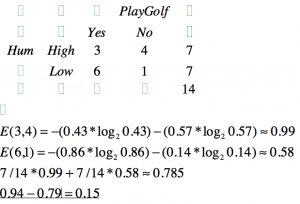
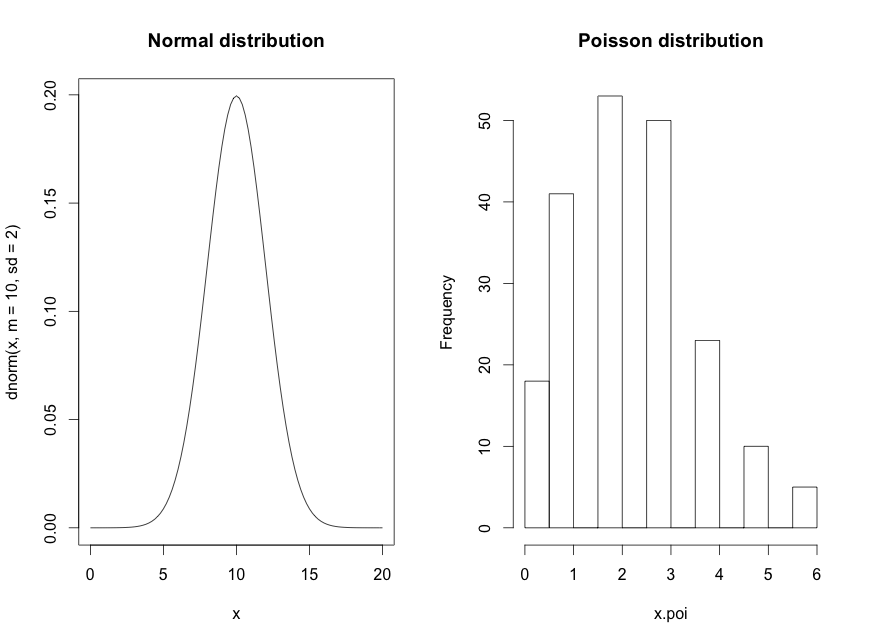
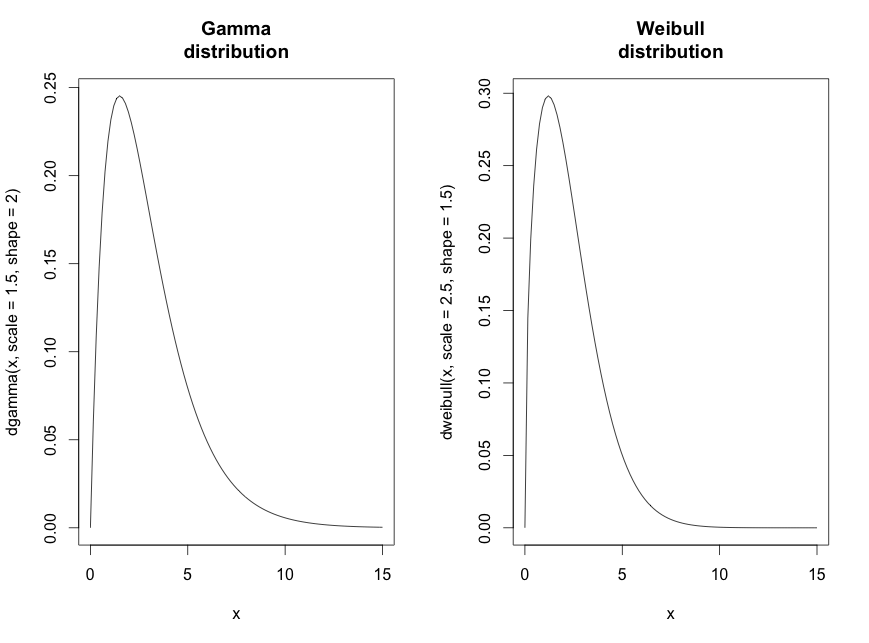
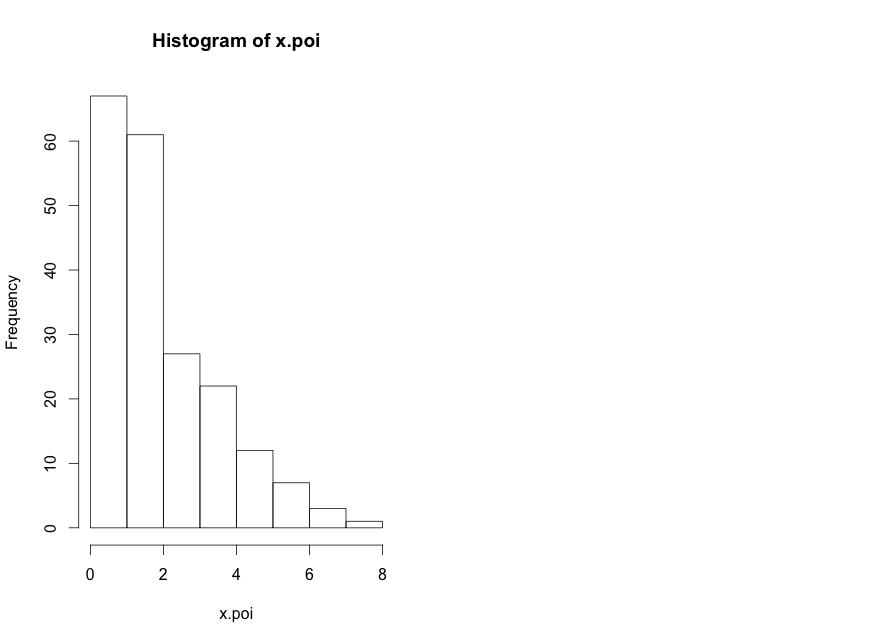
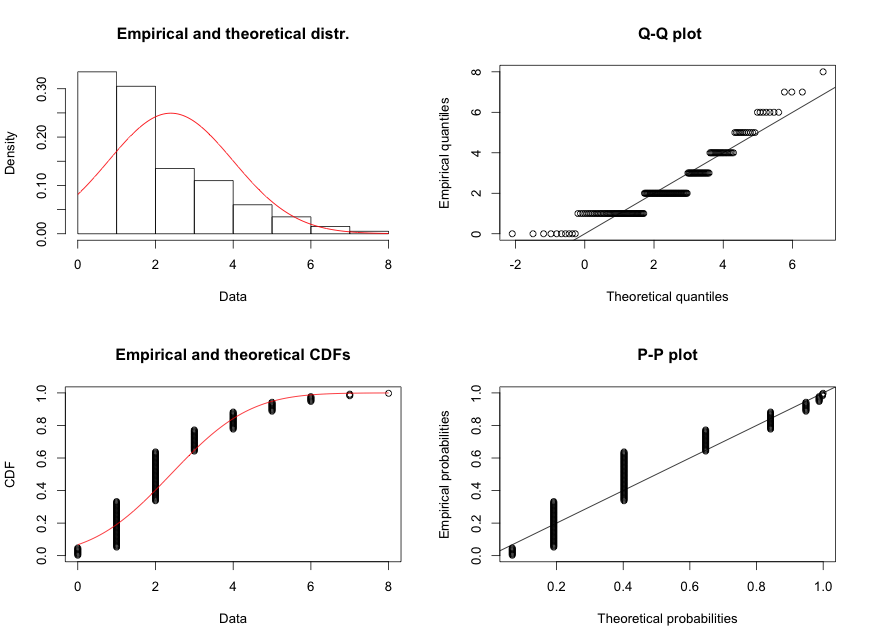
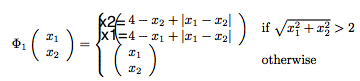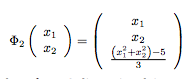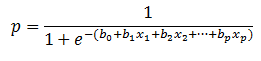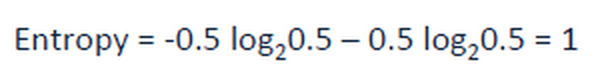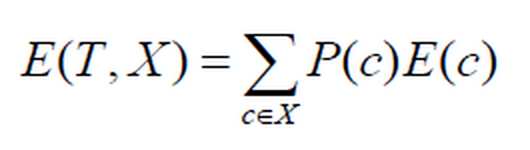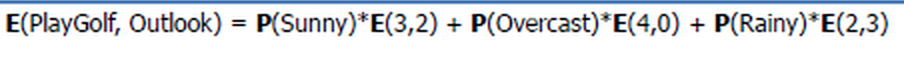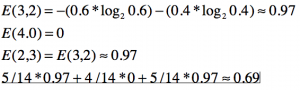Machine Learning – Page 4 – Margus Roo

SVM – Support Vector Machine

Posted on September 9, 2013 - September 11, 2013 by margusja

SVM (Support Vector Machine) püüab eristada n-dimensioonilises ruumis sarnaseid gruppe üksteisest, eristades neid joontega.

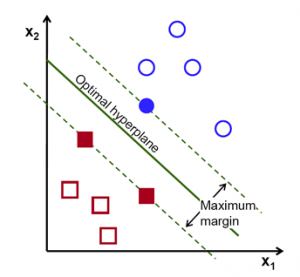
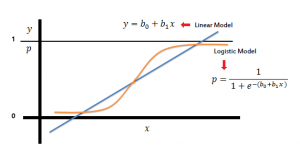
Parim joon (hyperplane rohkem kui 2D ruumis) on selline, mis asub kõikidest eristatud gruppidest võimalikult kaugel. Allpool oleval joonisel on selleks “Optimal hyperplane” joon

ehk y = wx+b

w – weight vector (kaalu vektor)

b- bias

x – punkt treeningsetis, mis on lähim hyperplane’le ehk punkte teeningsetis , mis on lähim hyperplanele, kutsutakse Support Vectoriks (e canonical hyperplane).

Support vectoreid on kõige raskem klassifitseerida, kuna nad on nn decision linele kõige lähemal.

x on vektor.

Optimaalne hyperplane on esitletav väga paljudel Bo ja Bx kombinatsioonidena –

Nüüd leiame kauguse hyperplane (Bo, B) ja punkti x vahel – 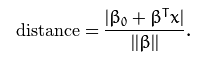* Antud juhul võib käsitleda valemis olevat avaldist ||B|| = |B| eg abs(b) (For complex numbers, Norm[z] is Abs[z].)

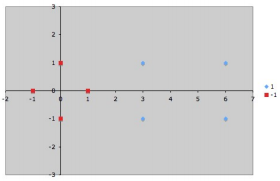
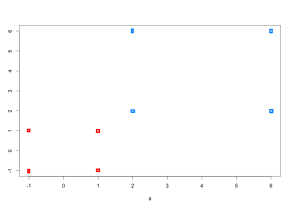
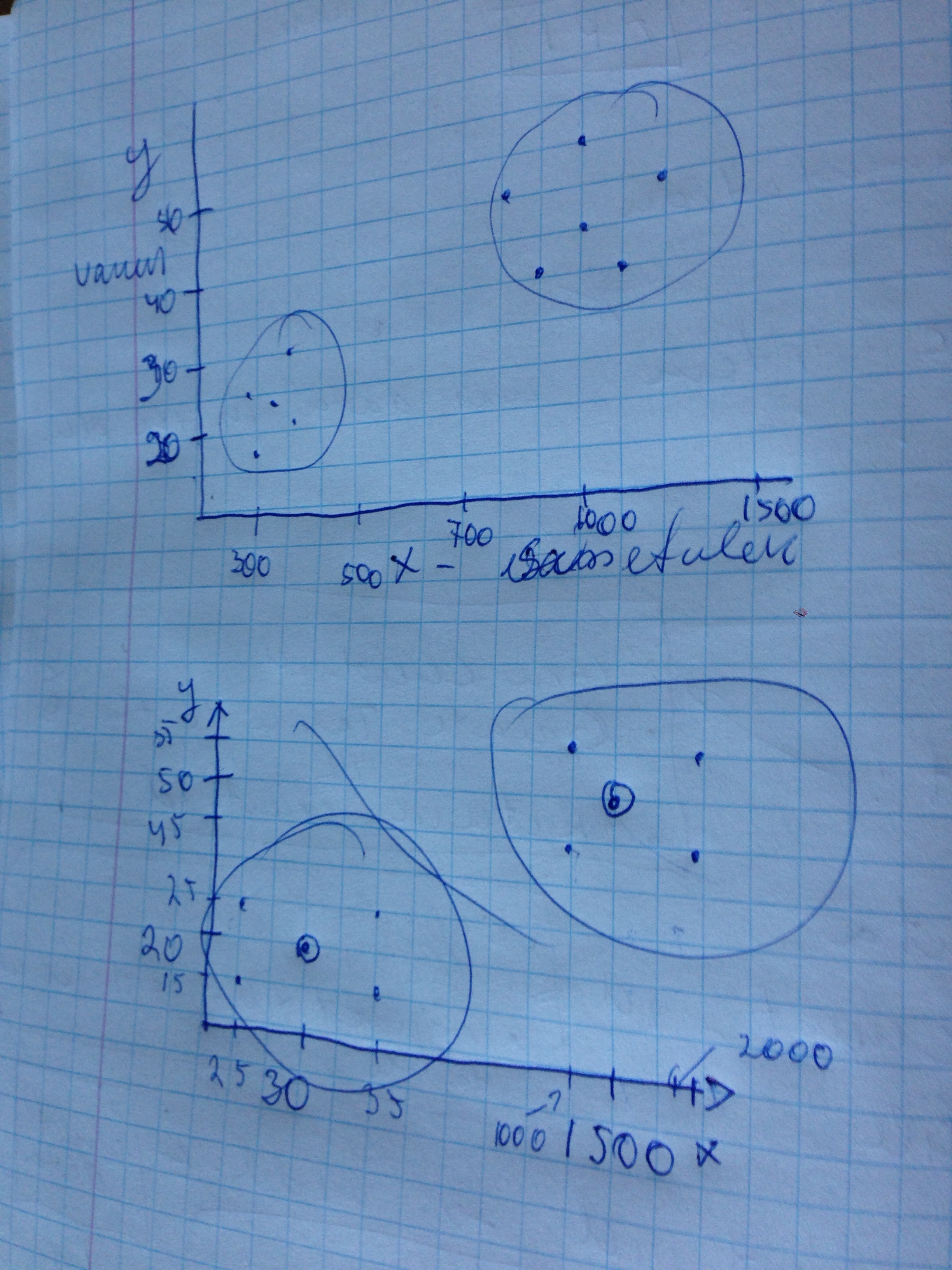
Võtame näiteks lihtsa andmehulga lineaarselt eraldatava R^2 ruumis:

Grupp 1 (+1) on: {(3;1), (3; -1), (6;1), (6;-1)}

Grupp 2 (-1) on: {(1;0), (0;1), (0;-1), (-1;0)}

On näha, et jaotus saab olla selgelt lineaarne ja support vektorid oleks antud juhul:

{s1=(1;0), s2=(3;1), s3=(3;-1)}

Valides bias (b) = 1 saame:

{s1’=(1;0;1), s2’=(3;1;1), s3’=(3;-1;1)}

Koostame võrrandisüsteemi:

a1*s1’*s1′ + a2*s2’*s1′ + a3*s3’*s1′ = -1 // tegu on -1 grupi (grupp 1) support vectoriga

a1*s1’*s2′ + a2*s2’*s2′ + a3*s3’*s2′ = +1 // tegu on +1 grupi (grupp 2) support vectoriga

a1*s1’*s3′ + a2*s2’*s3′ + a3*s3’*s3′ = +1 // tegu on +1 grupi (grupp2) support vectoriga

Teades s1′, s2′ ja s3′ saame:

a1*{1,0,1}*{1,0,1} + a2*{3,1,1}*{1,0.1}*a3*{3;-1;1}*{1,0,1} = -1

a1*{1,0,1}*{3;1;1} + a2*{3,1,1}*{3;1;1}*a3*{3;-1;1}*{3,1,1} = +1

a1*{1,0,1}*{3,-1,1} + a2*{3,1,1}*{3,-1.1}*a3*{3;-1;1}*{3,-1,1} = +1

Korrutame vektorid:

a1*2 + a2*4 + a3*4 = -1

a1*4 + a2*11 + a3*9 = +1

a1*4 + a2*9 + a3*11 = +1

…

a1=-3.5; a2=0.75; a3=0.75

w’ = a1*s1’1 + a2*s2′ + a3*s3′ = -3.5*{1;0;1} + 0.75*{3;1;1} + 0.75*{3;-1;1} = {-3.5;0;-3.5} + {2.25;0.75;0.75} + {2.25;-0.75;0.75} = {1;0;-2}

Kuna me laiendasime meie algseid vektoreid biase (1), siis vektori w’ kaks esimest elementi on w ja viimane element on b ehk y = {1;0}*x + -2 graafikuga:

, kus on nähe selgelt kolm (kollast) support vektorit ja neid eraldav arvutatud hyperplane.

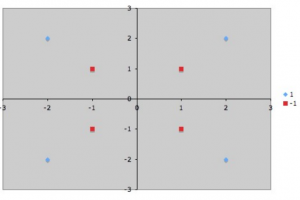
Siiani tegelesime lineaarse probleemiga. Kujutame seekord, et meil on selline andmehulk:

Group 1 (+1) {(-2;-2), (2;2), (2;-2), (-2;-2)}

Group 2 (-1) {(-1;1), (1;1), (1;-1), (-1;-1)}

mida saab 2D kordinaatteljestikul esitleda nii:

Mittelineaarse probleemi korral võib punktid anda teatud funktsiooni sisendiks, mis teisendab input space -> feature space

Näeme, et tingimusele sqr(x1^2 + x2^2) > 2 vastavad punktid {(-2;-2), (2,2), (2,-2), (-2,-2)} , mis kuuluvad gruppi +1. Funktsioon tagastab meile uue andmehulga:

Group 1 (+1) {(2;2), (6;2), (6;6), (2;6)}

Group 2 (-1) {(-1;1), (1;1), (1;-1), (-1;-1)}

Kanneme andut punktid kordinaatteljestikule:

Ja nüüd on antud andmehulka juba võimalik lineaarselt lahendada.

Võib kasutada ka tehnikat, mida kutsutakse Kernel Trick

Põhimõtteliselt anname input space ehk sisendandmetele juurde veel ühe mõõtme ja tekitame features space R^2 -> R^3

tulemusena tekib R^3 andmehulk:

Group 1 (+1) {(-2;-2;1), (2;2;1), (2;-2;1), (-2;-2;1)}

Group 2 (-1) {(-1;1;-1), (1;1;-1), (1;-1;-1), (-1;-1;-1)}

, mis on lineaarse(te) support vektoritega eraldatav.

Visuaalselt oleks see nüüd esitletav:

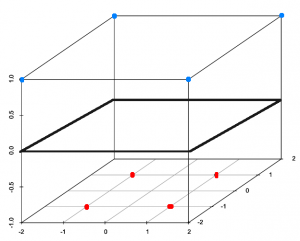, selgelt on nüüd eristatavad lineaarselt punased ja sinised punktid 3D ruumis.

SVM andmete ettevalmistamine:

Viia kõik tekstilised klassifikaatorid numbrilisele kujule
Scaling – aitab vältida olukorda, kus mõni atribuut domineerib teise üle.

Tuleb kindlasti eristada, mida otsitakse, kas regressioonimudelit või klassifitseerimist (SVM-Type: C-classification)

Mida praktilist SVN annaks?

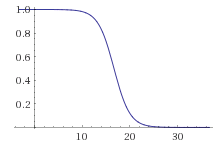
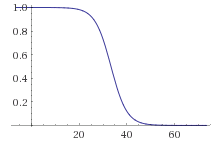
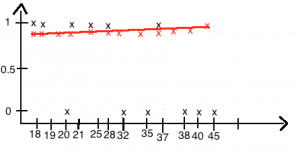
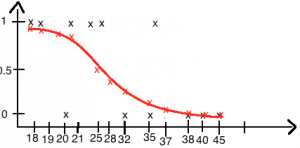
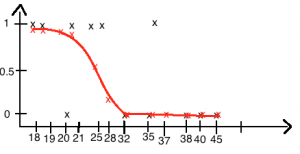
Oletame, et meil on hulk andmeid, mis iseloomustavad mingit objekti ja meil on iga objektiga seotud sündmus kujul 1 ja 0 e 1 tähendab, et sündmus toimus ja 0, et sündmus ei toimunud.

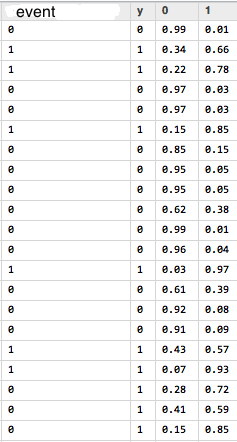
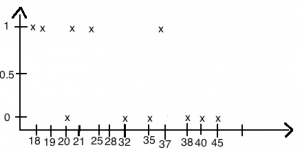
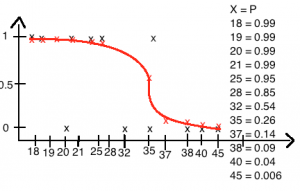
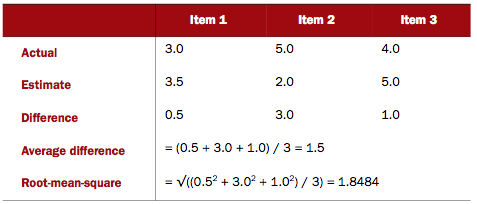
Kasutades SVN abi, saame näiteks alloleval pildil oleva info, mis kirjeldab:

event – reaalselt toimunud sündmus treeningandmetes; y – ennustatud event SVN poolt; 0 – sündmuse mittetoimumise tõenäosus; 1 – sündmuse toimumise tõenäosus

Logistic Regression

Posted on August 29, 2013 - August 29, 2013 by margusja

Logistiline regressioon on üks binaarse tunnuse analüüsimeetod, mis prognoosib uuritava sündmuse toimumise tõenäosust ja selle muutumist sõltuvalt pideva argumenttunnuse väärtuse muutumisest

Logistiline regressioon arvutab binaarse tulemuse tõenäosuse ühe või mitme numbrilise ja/või diskreetse faktori põhjal. Lineaarset regressiooni ei saa kasutada binaarse tulemuse tõenäosuse arvutamiseks, kuna tõenäosus ei oleks 0 ja 1 vahel, aga logistiline regressioon tagab, et uuritava sündmuse tõenäosus jääb alati vahemiku 0 kuni 1.

Põhivalem:

Konstant b0 liigutab logistilise regressioonigraafiku kõverat vasakule ja paremale.

Näiteks lineaarfunktsioon y=-0.1+0.2*x, mille graafik on:

funktsioon 1/(1+e^-(1-0.3*x)) argumendiga b0 = 1, annab graafiku:

Muutes b0 = 10, annab funktsioon 1/(1+e^-(10-0.3*x)) graafiku:

Muudame konstanti b0 – 0.1 -> 0.3, saame lineaarfunktsiooni y=-0.3+0.2*x, mille graafik on:

Konstant b1…bn mõjutab logistilise regressioonigraafiku kõvera nurka.

funktsioon 1/(1+e^-(10-0.6*x)), kus b1=0.6 graafik on:

Screen Shot 2013-08-29 at 5.49.45 PM

funktsioon 1/(1+e^-(10-0.3*x)), kus b1=0.3 graafik on:

Nagu eelnevalt mainisin, saab logistiline regressioon hakkama suurema hulga parameetritega:

Kindlasti tuleb toonitada, et arvutustulemus annab sündmuse toimumise tõenäosuse, mitte tõenäosus reaalse väärtuse suhtes!

Näiteks andmehulk, kus esimesel kohal on sõltumatu muutuja ja teisel kohal sõltuv muutuja:

X1,Y 18,1 19,1 20,0 20,1 20,1 21,1 25,1 26,0 28,1 32,0 35,0 37,1 37,0 37,0 38,0 40,0 45,0

annab sündmuse toimumise tõenäosused:

X1 Y Calc Prob 18.0000 1 0.8825 19.0000 1 0.8602 20.0000 0 0.8344 20.0000 1 0.8344 20.0000 1 0.8344 21.0000 1 0.8049 25.0000 1 0.6500 26.0000 0 0.6034 28.0000 1 0.5051 32.0000 0 0.3148 35.0000 0 0.2015 37.0000 1 0.1448 37.0000 0 0.1448 37.0000 0 0.1448 38.0000 0 0.1218 40.0000 0 0.0851 45.0000 0 0.0332

Selgelt on näha, et vanuse kasvades, tõenäosus saada Y=1 väheneb.

Kanname andmed X/Y koordinaatteljestikule

Proovime ise ka proovimeetodiga leida b0 ja b1 argumente funktsioonile 1/(1+e^-(b0+b1*x))

Katsetame b0 = 0.1 ja b1 = 0.1. Saame graafiku:

Antud juhul on kenasti näha, et valitud parameetrid b0 ja b1 ei toimi ja funktsioon ei iseloomusta sõltuvat muutujat peale sõltuva muutuja kasvamist üle 32.

Proovime b0 = 5 ja b1 = -0.2, tulemus on juba reaalsem.

Proovime b0 = 10, b1 = -04, nende parameetrityega oleks tarvis graafikut natukene paremale liigutada.

Nagu ma ülal mainisin, saab graafikut paremale ja vasakule liigutada b0 argumendiga.

Valime b0 = 13 ja b1 = -0.4, sest graafiku nn kumerus sobis meile eelmisel katsel. Tulemus on juba ideaalilähedane.

Loomulikult ei tule igapäevases toimimises niimoodi proovimeetodiga kordajaid otsida, samas on ülaltoodu hea selgitus kuidas logistiline regressioon toimib.

Decision Tree #2

Posted on August 27, 2013 by margusja

Oletame, et meil on mingi kogus informatsiooni ja me soovime tuletada reegleid, kuidas mingi tulemus on tekkinud ehk luua decision tree, nagu alloleval joonisel

Arvutame nn “Target” entroopia . Target jaguneb 5 X No ja 9 X Yes. Kokku on 14 kirjet. 5/14 ümardame ja saame 0.36. 9/14 ümardame ja saame 0.64.

Entroopia valem on

Meie puhul tuleb arvutus:

Nüüd otsime, millieses tulbas on kõige rohkem informatsiooni:

, kus T on target ja X on tulp.

Meil on neli tulpa: Outlook, Temp, Humidity ja Windy.

Outlook arvutamine:

Kasutame valemit:

Screen Shot 2013-08-27 at 7.40.07 PM

ehk:

0.94-0.69=0.25

Temp arvutamine:

Humidity arvutamine:

Windy arvutamine:

Selgus, et kõige rohkem informatsiooni sisaldab tulp outlook – 0.25. Siit saame joonistada välja esimesed harud:

Kuna Outlook -> Overcast target on igal juhil Yes, siis joonistub siit nn leht:

Siit edasi tuleb harud, mis sisaldavad entroopiat (suuremat, kui 0) edasi harutada Outlook > Sunny, saame info:

Kõik hakkab otsast peale. Arvutame target tulba entroopia:

Windy annab kahtlemata lehed Yes/No:

Tulemus:

Nüüd on jäänud haru Outlook > Rainy, mis sisaldab informatsiooni:

Siin võib kasutada juba visuaalset analüüsi:

Siit saame viimased lehed:

Decision tree meetodit on samuti pseodokeeles hea esitleda:

Decision Tree Part 1

Posted on August 15, 2013 - August 15, 2013 by margusja

Kujutame ette, et me peame valima kas avada ehitus- või elektroonikaäri. Teame, et valides ehitusäri oleks kasum 100 EUR ja valides elektroonikaäri kasuks, oleks kasum 90 EUR. Valik ei ole raske, loomulikult valiksime ehitusäri. Miks? Sest kasum on suurem.

Teeme asja natukene keerulisemaks.

Valides Ehitusäri, siis on õnnestumise võimalus 50% ja ebaõnnestumise võimalus samuti 50%. Kusjuures õnnestumise puhul on kasum 100 EUR ja ebaõnnestumise puhul kahjum -30 EUR.

Valides Elektroonikaäri, siis õnnestumise võimalus on samuti 50% ja ebaõnnestumise võimalus on 50%. Õnnestumise puhul on kasum 90 EUR ja ebaõnnestumise puhul kahjum -10 EUR.

Mõistlik valik oleks elektroonikaäri, sest siin on kasum võrreldes elektroonikaäriga natukene vähem, aga kahjum on samuti väiksem oluliselt, seega kogu risk väiksem.

Vaatleme ka seda otsust matemaatiliselt.

On näha, et eeltoodud muutujate korral, valides elektroonikaäri, siis on EELDATAV kasum 40 EUR. Eeldatava kasumi all peetakse silmas seda, et kui samade tingimuste korral teha ülaltoodud valikuid, siis paljude-paljude proovimiste korral on keskmine kasum, valides elektroonikaäri, 40 EUR.

Mahout random-forest-tree Describe -d parameter Detect CSV filetypes

Posted on June 18, 2013 - June 18, 2013 by margusja

A simple solution how to detect CSV filetypes

github link

Mahout ForestVisualizer

Posted on June 4, 2013 by margusja

regressioonianalüüsi tulemuse tõlgendamine R keskkonnas

Posted on May 31, 2013 - June 2, 2013 by margusja

> summary(fit)

Call:
lm(formula = mydata$mpg ~ mydata$cyl, data = mydata) // Mudel, mida kasutati

Residuals:
Min 1Q Median 3Q Max
-4.9814 -2.1185 0.2217 1.0717 7.5186 // Punkthinnangud

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 37.8846 2.0738 18.27 < 2e-16 *** // a
mydata$cyl -2.8758 0.3224 -8.92 6.11e-10 *** // sõltumatu muutuja korrutis – b

Estimated – Funktsiooni ennustatud koefitsendid, lineaarse regressiooni korral (y=bx+a) a ja b.

Std. Error – Screen Shot 2013-06-02 at 9.05.05 PM

// (t value korrelatsiooni põhjal arvutatud statistiku empiiriline väärtus)
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1 – alla 0.05 on statistiliselt olulised regressioonivõrrandis.

Residual standard error: 3.206 on 30 degrees of freedom
Multiple R-squared: 0.7262, Adjusted R-squared: 0.7171 // Determinatsioonikordaja – regressioonimudeli suutlikus kirjeldada mõõdetud suurusi skaalal 0 kuni 1.
F-statistic: 79.56 on 1 and 30 DF, p-value: 6.113e-10

p-value – Eksimuse tõenäosus sisukat (Enamasti H1) hüpoteesi eelistades. Mida väiksem, seda väiksem on eksimise tõenäosus. Harilikult alla 0.05 oleks soovitatav.

> mydata mpg cyl Mazda RX4 21.0 6 Mazda RX4 Wag 21.0 6 Datsun 710 22.8 4 Hornet 4 Drive 21.4 6 Hornet Sportabout 18.7 8 Valiant 18.1 6 Duster 360 14.3 8 Merc 240D 24.4 4 Merc 230 22.8 4 Merc 280 19.2 6 Merc 280C 17.8 6 Merc 450SE 16.4 8 Merc 450SL 17.3 8 Merc 450SLC 15.2 8 Cadillac Fleetwood 10.4 8 Lincoln Continental 10.4 8 Chrysler Imperial 14.7 8 Fiat 128 32.4 4 Honda Civic 30.4 4 Toyota Corolla 33.9 4 Toyota Corona 21.5 4 Dodge Challenger 15.5 8 AMC Javelin 15.2 8 Camaro Z28 13.3 8 Pontiac Firebird 19.2 8 Fiat X1-9 27.3 4 Porsche 914-2 26.0 4 Lotus Europa 30.4 4 Ford Pantera L 15.8 8 Ferrari Dino 19.7 6 Maserati Bora 15.0 8 Volvo 142E 21.4 4 > chisq.test(mydata)

Pearson’s Chi-squared test

data: mydata
X-squared = 46.1698, df = 31, p-value = 0.03908

Oletame, et me oleme võtnud eesmärgiks tõestada, et kahe tulba vahel (mpg ja cyl) on seos, siis H1 e alternatiivne hüpotees oleks, et kahe tulba vahel on seos ja Ho on, et seos puudub.
Kuna p-value on 0.03 e väiksem, kui 0.05, siis võime 5% eksimismääraga vastu võtta H1 hüpoteesi.

R – normaljaotus versus Poissoni jaotus versus gammajaotus versus Weidbulli jaotus

Posted on May 29, 2013 - May 29, 2013 by margusja

Andmeanalüüsi juures on jaotuste äratundmine väga oluline.

Siinkohal üks võimalus R keskkonnas

Normaaljaotuse puhul on siinkohal andmehulk pidev (loodud x.norm <- rnorm(n=200, m=10, sd=2)) ja Poisson jaotuse puhul on andmehulk diskreetne (loodud x.poi<-rpois(n=200,lambda=2.5)). Gammajaotuse puhul on on tegu pideva andmehulgaga. Genereeritud (dgamma(x, scale=1.5, shape=2)). Weidbulli jaotus on genereeritud dweibull(x, scale=2.5, shape=1.5)

* Teeme illustratiivse näite.

* Loome normaaljaotusega andmehulga x.poi<-rpois(n=200,lambda=2.5)

1 1 2 1 1 2 3 1 1 3 6 1 4 5 4 2 3 5 5 2 1 1 2 2 5 2 1 0 2 4 2 1 2 3 2 3 3 3 2 2 2 3 5 1 2 1 2 1 2 5 4 5 2 3 2 1 1 2 2 5 2 2 1 4 3 1 0 3 3 1 0 1 2 1 2 1 1 1 2 4 0 2 4 2 0 1 2 1 1 1 1 1 6 2 2 3 1 1 0 5 3 1 2 2 2 7 1 4 0 2 1 1 4 3 1 2 1 2 6 3 3 2 2 8 4 5 4 4 1 4 7 2 2 4 0 2 2 1 3 6 7 1 2 2 3 1 2 1 2 3 2 0 4 2 6 1 4 1 4 2 1 2 4 1 3 4 0 3 3 2 2 3 5 1 1 2 2 4 1 2 2 3 3 6 1 1 4 4 1 6 1 1 5 2 1 2 3 2 2 1

* vastav histogramm

* Kontrollime, milline oleks tulemus, kui me eeldaksime, et tegu oleks normaaljaotusega

Pole just eriti hea.

Kontrollime, kui me eeldame, et tegu on Poissoni jaotusega andmehulgaga

Nagu jooniselt näha on, palju parem. Oma andmete jaotusmudeli tundmine on oluline!

Näiteks soovides Pearsoni korrelatsioonikordajat leida Possoni jaotusega andmehulgast, siis ei pruugi see tegevus edasisteks analüüsideks vajaliku infot anda. Teatavasti saab lineaarset korrelatsioonikordajat arvutada noraaljaotusega andmehulga pealt.

Paberilt koodi

Posted on May 15, 2013 by margusja

Paberil oli selline plaan

Tekkis küsimus, kas minu kood ka asjast aru saab nii. Sai küll.

Root-mean-square näide

Posted on May 2, 2013 by margusja

Ülaltoodu demonstreerib väga ilmekalt, kuidas kasutada root-mean-square võimalusi.

Antud juhul on tarvis leida minimaalne root-mean-square, mis on parim ennustus teadaolevate andmetega võrreldes.